SSL Minutes

SSL Minutes

29 March 2001
Dominic Johann-Berkel

Baxter Permutations:

Dom presented information about Baxter Permutations:
In 1954, Eldon Dyer asked the following question: Let f and g be continuous functions that commute under composition (that is, f(g(x)) = g(f(x)) for all x). Let f and g map the unit interval [0,1] into itself. Must f and g have a common fixed point, meaning a point z such that f(z) = z = g(z)?
Though William Boyce ultimately proved this false, the investigation of Dyer's conjecture yielded interesting information. Specifically, if f and g do have a fixed point (in fact, if they have finitely many fixed points), then the pair of commuting functions induces a Baxter permutation.
If N denotes an odd natural number, I_N denotes the set of natural numbers through N, O_N the odd elements of I_N, E_N the even elements of I_N, and P is the permutation P: I_N --> I_N, then we can define a Baxter permutation as follows:
Def: P: I_N --> I_N is a Baxter permutation (Type I) of order N if and only if
1.) P(O_N) = O_N, P(E_N) = E_N;
2.) If P(n) is between P(2i) and P(2i + 1), then n = 2i;
3.) If P(n) is between P(2i - 1) and P(2i), then n = 2i.
(Note: This is the definition of what we have been calling a Type I Baxter permutation. At this point in my presentation, I should have defined a Type II Baxter permutation since the rest of my talk was primarily concerned with Type II Baxter permutations.)
Following the definition, I argued (admittedly, rather weakly) that there was a correspondence between Baxter permutations and thee non-intersecting paths. This correspondence consists of composing two bijections. The first one joins Baxter permutations and twin binary trees, the second one joins twin binary trees and three non-intersecting paths.
For the sake of simplicity, I will reconstruct my argument through a different (better) example. In class, I applied my argument to the following Type I Baxter permutation: 3 2 1 4 5 6 7. The paper which outlines the argument uses Type II Baxter permutations. Thus, I will proceed by examining a Type II Baxter permutation.
Def: A permutation P of Sn is a Baxter permutation (Type II) if and only if, for all integer m?[n - 1], P can be uniquely factorized by: P = P'.m.P<. P>.m+1.P'' or P = P'.m+1.P>.P<..m.P'' Where all the numbers of P< (respectively P>) are less than m (respectively greater than m + 1).
Thus, according to this definition, 4 2 3 6 5 7 1 is a Type II Baxter permutation of order 7. For example, for m = 4 we have P< = 2 3 and P> = 6. For m = 1, we have P> = 3 6 5 7 and P< = X. Etc.
Lemma: There is a bijection between Baxter permutations (Type II) on [n] = {1,2,,n} and twin binary trees. Proof: For simplicity's sake, I omit the proof. To see a copy of the proof, please see (S. Dulucq, O. Guibert, Mots de piles, tableaux standards et permutations de Baxter, 6th Formal Power Series and Albegraic Combinatorics Conf., Dimacs, 1994, Discrete Math., to appear).
Ex: Look at the Type II Baxter Permutation 4 2 3 6 5 7 1. According to the Lemma, there is a bijection between this permutation and a pair of binary trees. We show this bijection through an example:
           4 2 3 6 5 7 1

          1            7
	 / \          / \
        2            6   1
       / \          / \  |\
      4   3        4   5
     / \ / \        \  |\
            5        3
           / \      / \
          6   7    2
         / \ / \  / \
To form the first tree (the increasing tree), we start with the least value in the permutation, 1. Then we see where the next value, 2, is in relation to the one. It is to the left, so we draw a stem downward to the left. Next, we see where 3 is in relation to 2. It is to the right of 2 and still left of 1, so we draw a stem downward and to the right from 2. Next, where is 4? It is to the left of 3, but it is also to the left of 2. Thus, we will draw a stem downward and to the left from 2. 5 is to the right of 3. 6 is to the left of 5. And 7 is to the right of 5. Since each number in the binary tree must have two descending branches, one to the left and one to the right, we can add "leaves" to the binary trees as shown by the dotted lines. Thus, every number has either two descending stems, one descending stem and one descending leaf, or two descending leafs. To form the other, decreasing, binary tree, we start with the greatest value in the permutation, 7. We repeat the same process until we form another tree. The increasing and decreasing binary trees form a pair of twin binary trees.
Lemma: There is a bijection between binary trees and pairs of non-intersecting paths (there are more details, but for the sake of this discussion, this much will suffice).
Proof: Again, for simplicity's sake, I will omit the proof. See (S. Dulucq, O. Guibert, Baxter Permutations, 1998, Discrete Math., 180, 149).
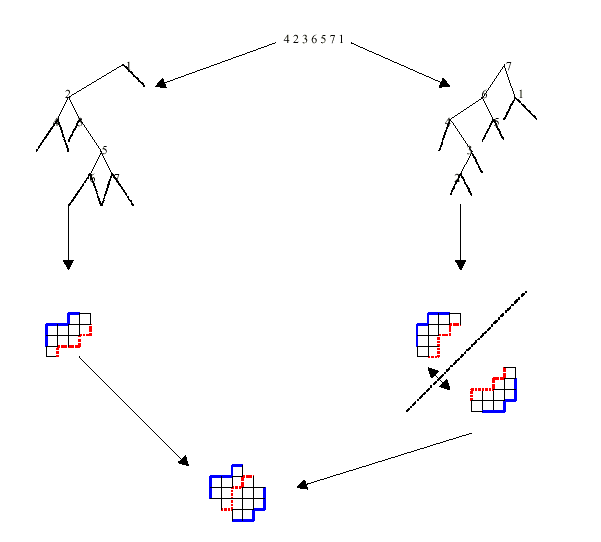
This correspondence is equivalent to travel in prefix order the completed binary trees and to code, respectively, the internal edges and the leaves. The first paths (shown in blue) are obtained by coding the internal left (respectively right) edges by a North (respectively East) step. The second paths (shown in red) are obtained by coding the left (respectively right) leaves (except the two extreme ones) by an East (respectively North) step.
Thm.: There is a bijection between twin binary trees and three non-intersecting paths.
Proof: According to our previous lemma, twin binary trees correspond to a pair of two non-intersecting
That about does it. That is what I attempted to demonstrate during Thursday's meeting. In hindsight, I would have done quite a few things differently, but I hope the preceding explanation helps clear things up. For information related to Baxter permutations, or to see more rigorous demonstrations of what I tried to talk about, please see any of the following articles:
W.M. Boyce, Generation of a class of permutations associated with commuting functions, Math Algorithms 2 (1967), 19-26.
S. Dulucq, O. Guibert, Mots de piles, tableaux standards et permutations de Baxter, 6th Formal Power Series and Albegraic Combinatorics Conf., Dimacs, 1994, Discrete Math., to appear
S. Dulucq, O. Guibert, Baxter Permutations, 1998, Discrete Math., 180, 143-156.
F.R.K. Chung, R.L. Graham, V.E. Hoggatt, M. Kleiman, The number of Baxter permutations, J. Combin. Theory Ser. A 43 (1986) 1-22.
I have more articles if you're interested, but these are the most interesting ones.