This is an abridged version of a longer FAQ list compiled by Joshua Abrams for Making Mathematics, an NFS - funded project based at Center for Mathematics Eductaion of Education Development Center (http://www2.edc.org/cme/).

• What is mathematics research?

• How do students benefit from doing mathematics research?

• For which students is research appropriate?

• What kind of support will I need?

• What do I need to do before I begin?

• What might a research sequence within a class look like?

• How does a research project end?

• How will doing research affect my workload?

• How can I balance the development of research skills with the need to cover specific mathematics topics?

What is mathematics research?

Mathematics research is the long-term, open-ended exploration of a set of related mathematics questions whose answers connect to and build upon each other. Problems are open-ended because students continually come up with new questions to ask based on their observations. Additional characteristics of student research include:

• Students develop questions, approaches, and results, that are, at least for them, original products.
• Students use the same general methods used by research mathematicians. They work through cycles of data-gathering, visualization, abstraction, conjecturing, and proof.
• Students communicate mathematically: describing their thinking, writing definitions and conjectures, using symbols, justifying their conclusions, and reading mathematics.
• When the research involves a class or other group, the students become a community of mathematicians sharing and building on each other’s questions, conjectures, and theorems.

How do students benefit from doing mathematics research?

Mathematics research influences student learning in a number of ways:

• Research provides students with an understanding of what it means to do mathematics and of mathematics as a living, growing field.
• Writing mathematics and problem-solving become central to student’s learning.
• Students develop mastery of mathematics topics. Philosopher and educator John Dewey claimed that we don’t learn the basics by studying the basics but by engaging in rich activities which require them. Research experiences require the repeated application of technical skills in the service of looking for patterns and testing conjectures. It is this repetition, in the context of motivating and meaningful problems, that leads to greater understanding and retention of mathematics skills. During an investigation, students make connections between ideas that further enhance retention.
• Students develop their own mathematical aesthetic as they practice making choices about which aspects of a problem to investigate.
• Students develop both confidence as mathematical thinkers and enthusiasm to do more mathematics. The creativity, problem-solving, surprises, and accomplishments that are part of research help to answer students’ questions about the value of studying mathematics. They are studying new methods so that they can answer their own questions. They are learning in order to do work that they care about at that moment (and not for a test or some far-off future task).
• Doing research is challenging and can be frustrating. Students’ commitment to persistence and tolerance for frustration grow as they are supported, encouraged, and given repeated opportunity to think about and succeed with problems over days and weeks.
• Students learn to distinguish between different levels of evidence and to be skeptical in the face of anecdotal evidence. The habit of looking for counterexamples to claims is a core skill for critical thinkers in all aspects of life.

For which students is research appropriate?

This question is usually more bluntly framed as "Can kids really do this?!" The experience of teachers in all types of school settings is that all children can successfully engage in mathematics research. In Making Mathematics, a recently completed project based at Education Development Center, teachers undertook research with urban, rural, and suburban students from grades 4 through 12. They guided at-risk, honors, and English as a Second Language (ESL) classes through projects lasting from a few weeks up to a year. Students in math clubs, individual students, and home-schooled students carried out successful investigations. One teacher first introduced research to her honors seventh graders. Once she was confident in her own experience, she tried the same project with two low-tracked eighth-grade sections. The quality of the questions, experimenting, reasoning, and writing was excellent in all three sections and indistinguishable between the honors and non-honors students. Research drew upon a richer array of student abilities than were assessed for tracking purposes.

Research can thrive in a heterogeneous class of students if you pick a project that does not require a lot of background to get started but which also inspires sophisticated questions. Students will pose problems at a level that is both challenging and appropriate for them.

How can I get my feet wet with research?

Making Mathematics teachers have been most comfortable trying research for the first time with one of their "stronger than average" sections. Some teachers have begun work with one or more interested students as part of a mathematics club or independent seminar. The purpose of these first excursions has been for the students to become familiar with the research process and for the teacher to see how students respond to lengthy, open-ended problem-solving.

You should commit at least three consecutive class periods at the start of a first investigation in order to maintain the momentum of the experience. You want students to appreciate that the questions are not typical quick exercises, so it is important that they get to wade into the work. Interruptions also make it harder for them to maintain a line of thinking. After the initial burst, you can sustain a project through weekly discussions of work done at home. If a problem is working well, do not be afraid to let kids pursue it for a long period of time.

What kind of support will I need?

Many teachers independently introduce research into a class. Your work will have greater impact on students if they encounter research in all of their mathematics classes. Both for that reason and in order to feel less isolated as you experiment, it is helpful to recruit one or more colleagues to try out research along with you. Share ideas and observations and even visit each other’s classes on days when the students are doing research. Talk with your department head or supervisor to garner support for your efforts.

Mathematicians in the Focus on Mathematics program would all be eager to serve as a mentor for you and your students. The rest of this paragraph describes how you might search for a mentor if independently of FOM. If you want an advisor for yourself or an outside audience for the work that your students do, you can contact the mathematics or mathematics education department at a local college and ask if any of the professors would be willing to serve as a mentor (either via email, phone, or in person) for you and your class. We have also found good mentors contacting corporations that employ scientists and mathematicians. Your mentor may just communicate with you or she may be willing to read updates or reports from the students and provide responses. You should make these exchanges via your email account—parental consent is required by law for direct internet communication. Be sure to let any prospective mentor know what your goals and expectations are for the students and for their involvement.

Mentors can help in a number of ways. They can:

• Help pick an area of inquiry and establish goals.
• Make suggestions about next steps (e.g., when to apply a research technique or content area, whether to redirect a class^’s efforts).
• Ask clarifying questions about the student^’s mathematical statements.
• Help students learn how to prove their claims.
• Study and reflect upon student work with you.
• Provide an authentic outside audience for student efforts.
• Provide emotional support such as encouragement, perspective, and advice.
• Identify resources.

What do I need to do before I begin?

• If you have never done any mathematics research yourself, it is time to join in! Your FOM mathematicians will help you and your colleagues, pick a project, and start your work looking for patterns, trying to state clear conjectures, searching for proofs or disproofs, and studying new, related problems. Many Making Mathematics teachers have found the summer a good time for professional growth via a research project.
• Decide what your goals for your initial foray are (e.g., each group will be responsible for posing and resolving one question or students will each have their own conjecture) and how much time you plan to spend on the project.
• Pick a project topic.
• Since research is unfamiliar to many parents, you may want to anticipate any questions that will arise by discussing your plans ahead of time. You can send a letter home to parents that helps them to understand what you will be doing and why.

What might a research sequence within a class look like?

The teaching notes accompanying the Making Mathematics projects (http://www2.edc.org/makingmath/) can serve as models that you can adapt to other projects. As noted earlier, it is best if you can introduce research with a burst that permits a coherent presentation of the research process before separating discussions with several days of non-research studies.

Once research is underway, each student or group of students may work on different, but related, questions. During whole-class discussion, classmates should describe the different problems that they are exploring. Students should report back on their progress (new questions, conjectures, proofs, etc.) periodically.

At the end of a class session devoted to research, each group should give themselves a homework assignment in a logbooks. You can check these recorded tasks to make sure that the assignments were meaningful and check the subsequent entry in the logbook to make sure that the student made reasonable progress with the tasks. Typical homework challenges include:

• Extend a pattern, generate more data.
• Try to prove a particular conjecture.
• Test a bunch of conjectures with different cases to see whether counterexamples can be found.
• Try to find a formula or rule for a pattern.
• Identify and learn about areas of mathematics that might be helpful to the investigation.
• Read about related problems and how they were solved.
• Pose extensions of the project.

Students can think about where they are in the research process (see below for one model for the process) in order to decide what step to attempt next. Their work should have some narrative explanations ("I did this because…"). Students can work on their homework for a few days, but groups will also need regular class time to catch up on each other’s thinking, to work together, and to then coordinate next steps before their next stretch of independent work.

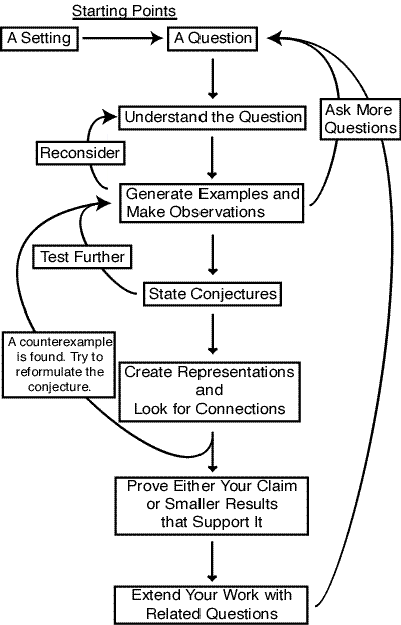
Although some projects, such as the one in Making Mathematics include teaching notes of some kind that suggest what to do on the first day, the second day, and so forth, you will need to pace the phases of a particular investigation according to the length of your class periods and the timing of a given class’s particular questions and discoveries. Here are some other decisions that you should be alert to as work proceeds:

• Students will naturally exhibit important research skills such as posing a conjecture, organizing data in an effective manner, or inventing a new definition. When this happens, you want to identify the skill and discuss its importance to research. For example, a student might note the existence of a counter-example to a classmate’s conjecture. If students do not already know about counter-examples, you could stop to highlight the contribution and do a side lesson on examples (generating test cases, remaining skeptical in the face of confirming examples, extreme and degenerate cases, and counter-examples).
• Issues will arise unpredictably and student comments may simultaneously pull a class in a number of possible directions. For example, one student may invoke a counter-example for the first time and another might pose two new questions to explore. Where do you head first? You should try to strike a balance between developing a formal understanding of research skills and allowing the research process to unfold without too many interruptions. It is always good to at least give a name to a new research skill or problem-solving strategy when a student demonstrates it. You can then return to a discussion of the considerations associated with that habit in depth at a later time.
• As an investigation continues, the difficulty of generating further examples may become an impediment to further progress. You should help the students decide whether carrying out the steps needed to find new examples is still itself illuminating or whether just the data gleaned from the examples is what they need. If the latter is the case and there is a way to use technology to speed up the work, it might be worth taking the time to teach the class or a particular group how to use the appropriate tool. For example, they might benefit from assistance doing symbolic manipulations using a computer algebra system (CAS), geometric constructions using a dynamic geometry program, or finding numeric examples using a spreadsheet.

As a class works thorough its early research experiences, be sure to document for them as much of their work as possible. Posters listing the students’ conjectures, questions, and theorems help students grasp the cyclical nature of the research process. They see how their different questions connect and build upon each other and learn which research methods are most helpful at which stages of an investigation. After these beginning projects, students are ready to work more independently and should be encouraged to pose their own questions for research.

How does a research project end?

A project can end when a student or group has resolved some central question. Often, there are many questions and, after good progress with some of them, students’ enthusiasm for the others may wane. You may have established certain goals for students: to create a proof, to generate a few clear conjectures, to pose a new problem and make progress with it. Each of these possibilities is a reasonable time for work on a project to end. Students can come to a satisfying sense of closure even with a project that leaves many unanswered questions. That feeling can be enhanced if they write a final report that summarizes their main questions and work and that concludes with a list of possible extensions worth exploring. The FOM mathematician can help you with ideas about formal write-ups for students who have engaged research project.

How will doing research affect my workload?

Ultimately, research is no more demanding on your time than teaching that is more traditional. In some cases, it shifts the balance so that you spend less time preparing lessons and more time responding to student work. If you have not taught research before, there will be an initial need to think through the different issues that will arise in class. This work will prepare you to take advantage of any "teachable moments" (student comments that can lead the class to new understandings). The Making Mathematics teacher handbook is a valuable resource as you develop experience doing research with students.

One strategy for managing the demands of teaching research is to keep good notes on your observations during class. Thorough ongoing documentation will facilitate the comments that you need to make when you collect work because you will have a good sense of the entire research process that an individual or group has gone through. The more often you can read and respond to student’s entries in a their logbooks, the better, but you do not have to collect everyone’s work all at once. You can sample a few each night. Lastly, having each group submit a single final report reduces the number of papers that you need to study to a manageable number.

How can I balance the development of research skills with the need to cover specific mathematics topics?

Teacher: Since I have a curriculum I have to cover, which really takes the whole school year, how do I cover that curriculum while implementing those problems that deepen the understanding of the required curriculum and is there some way to perhaps replace chunks of my text with such problems? I find balancing what I WANT to do and what I MUST do very difficult.

Mentor: I appreciate your frustration about the tension between covering technical content and giving your students the opportunity to learn about the process of doing mathematics. There is no question that teachers are being asked to whiz through too many topics. I try to remind teachers of what they already know: when we go too quickly, the material is not mastered well and so we are not being efficient.

The above exchange between a Making Mathematics teacher and her mentor is typical of the most common and emotional question with which teachers interested in research have grappled. Many have expressed stress at feeling trapped by competing demands. In some cases, the answer is simple: if there is a major state test next week and you need to cover five topics, it is definitely a bad time to start research. But, if you are months away and you consider how often students forget what they have studied, now is a good time to introduce your students to mathematics investigations.

"There is, of course, a cost to having the students engage more deeply in the mathematics: one "covers" less. However, when the payoffs include much deeper understanding, much longer retention of the content, enthusiasm, and the fact that the students get a much better sense of the mathematical enterprise, the price in (ostensible) coverage is a small one to pay." – Mathematics Educator Alan Schoenfeld.

The content versus research question reflects a false dichotomy. We know how fruitless it is to teach disconnected topics. If you do not use knowledge in active ways that allow you to make meaning of what you have learned, you do not retain that learning. Why do students seem to forget so much of what they study? Sometimes, they still have the skills but are only able to apply them when prompted (e.g., "I am doing a chapter four problem" or "I was told to use triangle trigonometry techniques"). Sometimes, the learning experience was not memorable (consider what you have remembered and forgotten from high school and try to identify why). The more research work becomes a strand throughout a course and a school’s curriculum, the better the interconnections between, and mastery of, technical content will be.

The NCTM Standards include many important goals (e.g., being able to conjecture, show persistence in problem solving, develop mathematical models, etc.) that we are supposed to "cover" that do not fit well in the framework of timed tests.

So, how do we combine research and technical content goals and what are some of the challenges that we face in our efforts? We can choose a research problem that will reinforce technical skills that a class has already studied. Alternatively, we can pick a problem that will introduce our students to and help them develop an understanding of a new topic. For example, we could use the Game of Set research project in place of or after a textbook introduction on combinatorics.

One problem that arises when using a research experience as a way to develop or reinforce a particular technical skill is that students’ questions and methods may not head in the direction that you expected. If you tell students to use a particular technique, then you short-circuit the research process. You are also risking turning the effort into a planned discovery activity, which usually lacks the motivational and intellectual power of true research.

You can address this problem in a few ways. A careful choice of project or framing of the question can often make certain skills inevitable. For example, a high school class proving theorems about Pythagorean Triples would be hard pressed to avoid using algebraic expressions or thinking about factors. You can also add your own questions to the class’s list. This makes you a participant in the process and assures that the class will spend some time on the issues that you want considered. Alternatively, you can let the students’ work take them where it will knowing that some other important area of mathematics is being developed or reinforced that you will not have to spend as much time on in the future. Then, after the research is over, you can return to the topic that you originally had in mind.

When students do get to follow their own intellectual muse, they are more likely to experience a wide range of mathematics topics. For example, in a class of fifth graders working on the Connect the Dots project, one student asked what would happen if each jump was chosen randomly. The shapes were no longer as attractive, but the question of whether they would ever close led to the idea of expected value. An independent research project on randomness in DNA led a student to study matrices and Markov processes. Students will teach themselves a chapter of content from a textbook if they think it will help them on a task about which they care.