The elements have been classified an organized on the periodic table.  The electron configuration for most elements can be easily obtained from a standard periodic table if the table is visualized as being divided into s, p, d, and f regions as illustrated below.

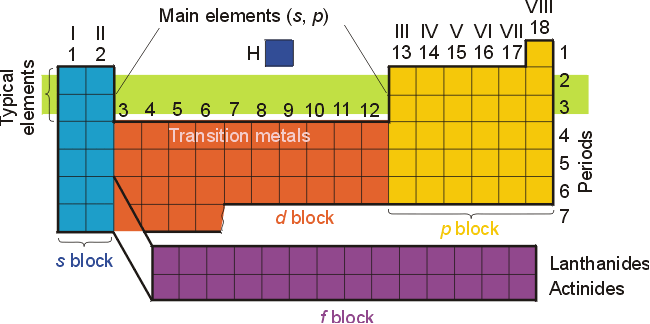
    The relative positions of the elements, and a thorough understanding of atomic orbitals and electron configuration can lead to many generalizations concerning a given element's properties and chemical behavior.  For example, metals usually react with non-metals to form hard crystalline (ionic) solids.  When metals react with other metals, the resulting alloy will have properties similar to the two metals involved.  Non-metals react with non-metals to form volatile compounds.
    A qualitative understanding of wave functions for the atomic orbitals and their properties is essential for explaining a variety of atomic properties such as size, ionization energy, electron affinity, electronegativity and polarizability.  The nature of each type of atomic orbital and it's proximity and penetrating ability towards the nucleus are key to understanding the energies of atomic orbitals and the resulting electron configurations.

    There are a few key features of atomic orbitals which will help you understand the properties of atoms.  Of particular interest are the amplitude of the radial wave functions near the nucleus, the number of radial nodes (locations where the radial wave functions pass through zero), and the radial distribution functions of the orbitals.  [The radial distribution function illustrates the probability of finding an electron a given distance from the nucleus.]  Although atoms contain many protons and electrons, the basis of all wave functions comes from hydrogenic orbitals, or orbitals for atoms with only one electron.  It is important to note that only the value of n, the principal quantum number, dictates the energy of orbitals in hydrogenic atoms (or ions).  Thus, the 2s and 2p orbitals are degenerate, having identical energies.  Likewise, the 3s, 3p and 3d orbitals will be degenerate.  We know that in multi-electron atoms, these orbitals have different energies.  We must consider the wave functions of the orbitals, and their proximity to the nucleus.  Orbitals which can penetrate closer to the nucleus will have lower energies than those which are at greater distances from the nucleus.
    Certain characteristics of s orbitals are unique.  All s orbitals have a finite (non zero) amplitude at the nucleus, as seen in the radial wave functions.  Other orbitals have a zero amplitude at the nucleus.  This results in significant electron density close to the nucleus in all s orbitals.
    A second feature is that of radial nodes.  All orbitals decay exponentially at sufficiently great distances from the nucleus, but some oscillate through zero.  These oscillations are called radial nodes.  The number of nodes = n-l-1 (where n=principal quantum number, l = orbital angular momentum quantum number).  For a 1s orbital, n=1, l=0, and there are no radial nodes.  A 2s orbital had 2-0-1 or 1 radial node.  For a 2p orbital, there are 2-1-1 or no radial nodes, whereas a 3p orbital has 1 radial node.  These features are illustrated below.

 
 

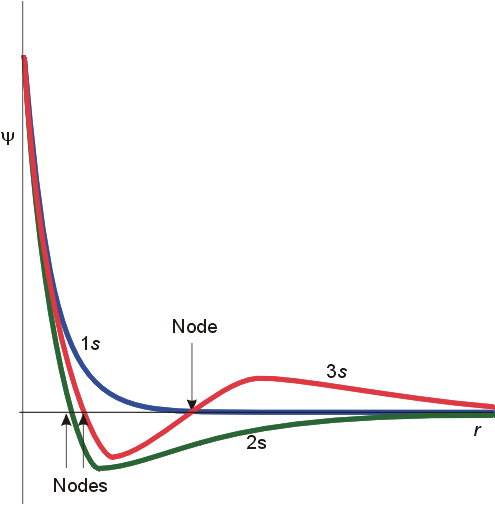
       The important differences are in the finite amplitude at the nucleus for the s orbitals, and the number of nodes for each orbital.  To fully understand the differing spatial orientation and penetrating ability of s and p orbitals, the radial distribution function is used.  This function illustrates the probability of finding the electron at varying distances from the nucleus.  The radial distribution functions for a 2s and 2p orbital are illustrated below.

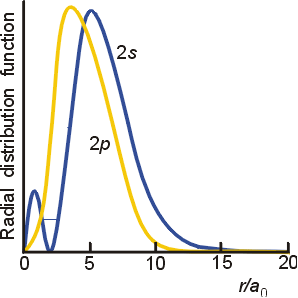
    On average, the 2s electrons will be at a slightly greater distance from the nucleus than the 2p electrons.  However, the 2s electrons have a higher probability of being closer to the nucleus due to the inner peak.  As a result, the 2s orbital will lie lower in energy than the 2p orbital in multi-electron atoms.  This is reflected in electron configurations for atoms in the second period and beyond on the periodic table.

    In multi-electron atoms, electrons are attracted to the nucleus and repelled by each other.  Consider a 3 electron atom.  The third electron will experience a lesser nuclear charge than the electrons in the 1s orbital, due to the shielding of the nucleus by the 1s electrons.  The third electron experiences an effective nuclear charge, Z_eff, which is equal to the total nuclear charge, Z, less the shielding, s.  Z_eff =Z-s
    The extent of shielding will depend on the radial distribution (or orbital type).  Since the 2s electron has a finite probability of penetrating the 1s orbital, there is not a large difference between the effective nuclear charge and Z.  That is, shielding is minimal.  A p orbital is less penetrating due to the nodal plane at the nucleus.  (The value of the radial distribution is zero at the nucleus.)  As a result, a p orbital is more shielded by the inner 1s orbital electrons than the 2s orbital is.

    Many atomic properties can be related to position on the periodic table.  The first is electron configuration, which is directly related to an element's position in the table.  [See the periodic table above.]  The Aufbau Principle and Hund's Rule dictate that electrons will occupy orbitals which are lower in energy.  When the orbitals are degenerate (of the same energy), the electrons will go in separate orbitals with parallel spins.  The parallel spins are a result of spin correlation, which is the tendency of two electrons with parallel spins to stay apart from each other and hence repel each other less.  There are some exceptions to the rules, notably in chromium and copper.

    The relative sizes of atoms or ions can be linked to position in the periodic table.  In discussion radii of atoms, the means of obtaining them must be specified.  Metallic radii are usually determined using X-ray data to determine the inter nuclear distances in metallic crystals.  Covalent radii are half the inter nuclear distance in covalent molecules.  If multiple bonding is possible, the bond length will reflect this.  Ionic radii are determined by measuring inter nuclear distances in ionic crystals.  An arbitrary reference radius must be set for one ion, and the other ions can be compared to the standard.  Usually the oxide ion is usually assigned a radius of 1.40 angstroms.
    The general trend is for atomic radii to decrease going across a period, and to increase going down a group or family.  In comparing the radii of elements in the 6th period (La to Hg) to those of the 5th period, there is almost no difference in size due to the Lanthanide contraction.  As the electrons in the f subshell are added, the value of Z_eff increases due to the added protons in the nucleus and the poor shielding ability of the f orbitals.  A similar contraction occurs in the d-block as well.
    In comparing ionic radii, all anions are larger than their neutral atoms, and all cations are smaller.

Copyright ©1998 Beverly J. Volicer and Steven F. Tello, UMass Lowell.  You may freely edit these pages  for use in a non-profit, educational setting.  Please include this copyright notice on all pages.