Molecules are assigned to point groups based on the number and orientation of their symmetry elements.  A scheme for determining the correct point group is provided in your text.  Highly symmetrical molecules (octahedrons or tetrahedrons) have their own point groups (O_h and T_d respectively).  Square planar molecules or octahedrons with different atoms on one axis are in the group D_4h.  Trigonal planar and trigonal bipyramidal molecules are D_3h.

    Certain physical properties of molecules are clearly linked to molecular symmetry.  Molecules which are symmetrically bonded to the same elements will not be polar, due to the canceling dipole moments.  Likewise, chirality (left or right handedness) is clearly a symmetry property.  Chirality can only be present in molecules which lack an improper axis or rotation.  Molecules with a center of inversion or a mirror plane cannot be chiral.
    The symmetry properties of molecules are tabulated on character tables.  A character table lists the symmetry elements of the point group, along with characters which are consistent with the different symmetry operations of the group.  The table characterizes how various atomic properties (the symmetry of atomic orbitals, rotations about axes, etc.) are transformed by the symmetry operations of the group.  The table for the C_3v group is provided below.  This group includes molecules such as ammonia, where there is a three-fold axis of rotation which also includes mirror planes (called vertical planes since they include the axis of rotation).
 
 
 

    There are many important features to the character table.  The standard convention is to specify the major (if there is more than one) axis of rotation as the z axis.  You'll note that the table says there are 2C₃ axis.  These represent rotation by 120⁰ and rotation by 240⁰ (or by -120⁰).  There are 3 vertical planes of symmetry, each going through the central atom and one of the other atoms.  The symmetry properties of each of these planes is the same, so they are grouped together.  The characters (usually integers and zeros) represent how various orbitals or rotations are transformed by the various symmetry operations of the group.  The set of characters in the A₁ set show that the p_z orbital on the central atom is unchanged by all of the symmetry operations.  When the orbital is unchanged, a character of +1 is used.  Note that s orbitals, which are totally symmetrical always transform as the A₁ set and are usually omitted from the list on the right.  The list to the right of the table also indicates that the functions x²+y² and z² also remain unchanged by all the symmetry operations of the group, and thus are represented by the A₁ character set.  If an orbital is unchanged, it will have a character of +1, if it changes sign, the character will be -1.  If a more complicated change occurs, the character will be 0.  The second set of characters, A₂, has the same symmetry properties as rotation about the z axis.  That is, rotation will remain the same under the operations of identity or rotation about the principal axis of rotation, but will be reversed by the mirror plane which runs through the z axis.  The last set of characters, E, has a few interesting features.  The character of 2 in the first column indicates that it is double degenerate.  This means that pairs of orbitals or rotations will be represented in this character set.  The use of parenthesis in the column to the right of the table indicates that the x and y axes, together, are represented by this set of characters.  (Likewise for the other orbitals and rotations paired within the parenthesis.)
 

    Symmetry considerations can be used to determine the hybridization of the central atom.  The process involves obtaining a set of characters which transform as vectors representing the sigma bonds in the molecule.  The set of characters, called a reducible set, is a linear combination of the irreducible representations found in the character table for the molecule.  The method can be outlines as follows:
 

1.   Determine the point group of the molecule.

2.  Consider the bonds as vectors, and determine how they are transformed by the symmetry operations of the group.  The character for each operation will simply be the number of vectors which remain in position while each symmetry operation is performed.  This set of characters is called a reducible set.

3.  Reduce the representation obtained into a linear combination of sets which appear in the character table for the group.

    The process outlined above will yield a set of characters which can be reduced to combinations of the sets of characters in the table for the appropriate point group.  In simple point groups, the reduction can sometimes be done by inspection.  In any case, the process of reducing representations is quite simple.  It is determined using the following formula.

• Problem: Determine the characters for the reducible character set which represents the hybrid orbitals of of the molecule BF₃ (point group D_3h).  Reduce the representation to obtain the hybridization of boron in the molecule.

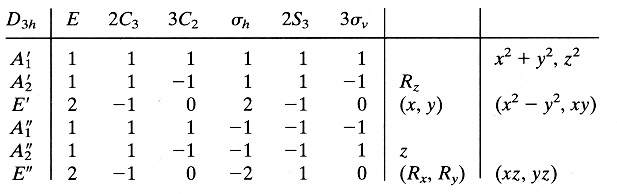
    The character table for the D_3h point group has an order (h) of 12, because there are a total of 12 symmetry operations for the group.  The above table and the worksheet below can be used to reduce the representation for the hybrid orbitals into the linear combination of some of the irreducible representations on the table above.  The orbitals corresponding to these irreducible representations will be listed on the right side of the character table.
 
 
 

    A similar treatment can be performed to consider the orbitals used in p bonding in the molecule BF₃.  Since the z axis is the one perpendicular to the plane of the molecule, we can consider how the p_z orbitals on each of the fluorine atoms are transformed by the symmetry operations of the group.  A character of +1 indicates that the orbital is unchanged by the operation.  A character of -1 indicates that the orbital has been inverted, and a character of 0 indicates that the orbitals on different atoms have been interchanged.  This produces the reducible set below.
 
 

    Group theory can also be used to determine the types of vibrations present in a molecule, and whether they will be observed in the UV or Raman spectra of the molecule.  A reducible representation which represents all of the types of molecular motion is produced.  This representation includes translations, rotations and vibrations.  It is obtained by examining how the cartesian coordinates (x, y, and z axes) are transformed by the symmetry operations of the group.  For any molecule, the total number of degrees of freedom (rotations, translations and vibrations) is equal to 3N, where N is the number of atoms in the molecule.  For linear molecules, 3 of these degrees of freedom arise from translations along the x, y and z axes, and two are the result of molecular rotations.  For non-linear molecules, there are three degrees of translational freedom and three degrees of rotational freedom.  The results are summarized below.

• Linear Molecules:  modes of vibrations = 3N-5
• Non-linear Molecules:  modes of vibrations = 3N-6

    The symmetry of all molecular motion is obtained by viewing each atom as the center of 3 intersecting axes (x, y and z).  The characters of the reducible representation will be related to the changes in these axes as each symmetry operation is performed.  If an atom is shifted by a symmetry operation, its contribution to the character is 0.  If an axis on an atom is shifted to its negative, that atom contributes a -1 towards the character for that operation.  If an axis is unchanged by a symmetry operation, its contribution towards the character for that operations is +1.  Once the characters are obtained, they are reduced by the previously described method.  A total of 3N representations are obtained.  From this set of irreducible representations, the sets relating to molecular translations and rotations are eliminated, leaving only representations due to molecular vibrations.
    The method will be illustrated using water, or any molecule belonging to the C_2v point group.  The character table for the group is provided below.  The orientation of the molecule is such that the molecule lies in the xz plane.  Please note that some texts will orient the molecule differently, with the molecular plane being the yz plane.  (I will always specify the molecular plane for a molecule of this type during an exam.)  The C₂ axis of rotation is along the z axis of the oxygen atom.
 
 

    If each atom is considered as the center of a set of cartesian coordinates, the identity element will leave all 9 axes unchanged, so the character will be 9.  The C₂ axis passes through the O atom along the z axis.  It exchanges both hydrogens, and reverses the x and y axes on the oxygen while leaving the z axis unchanged.  As a result, the character for this operations will be -1 (+1 for the z axis, and -1 for the y axis and the x axis).  The  xz mirror plane in which the entire molecule lies will cause each atom to have a reversed x axis while maintaining the x and z axes.  Each atom contributes +1 towards the character, or a total of +3 for the three atoms.  The mirror plane which lies in the yz plane passes through the oxygen atom and interchanges the hydrogen atoms.  The y and z axes on the oxygen atom are left unchanged, while the y axis is reversed.  Thus the character for s_yz is +1.    The reducible representation for all modes of molecular motion is summarized on the worksheet below.
 

    The set reduces to: 3 A₁ + 1 A₂ + 3 B₁ + 2 B₂.  These representations include molecular translations and rotations.  Translations transform as x, y and z, so A₁, B₁ and B₂ representations can be subtracted.   LIkewise, rotations transform as R_x, R_y and R_z, so the representations A₂, B₁ and B₂ can be subtracted.  The resulting molecular vibrations have the following symmetry:  2 A₁ and B₁.  For a simple point group such as C_2v, examination of the symmetry of each of these representations can easily lead to the following  representations of molecular vibrations.  The vibrations consistent with the A₁ symmetry are the symmetrical stretch and the symmetrical bend.  These are illustrated below and labeled as n₁ and n₂ .  The vibration mode with B₁ symmetry is the third representation.  The wave numbers for each vibration can only be determined experimentally.

    Once the symmetry of the molecular vibrations has been obtained, predicting whether the vibrations can be seen in the infrared and/or Raman spectra is quite simple.  Vibrations which are infrared active much involve a change in the dipole moment of the molecule.  The dipole vector transforms as x, y or z.  Since the symmetry representations for the vibrations in water has either z (for the 2 A₁ modes) or x (for the B₁ mode) as a basis, all three bands will infrared active.  For vibrations to appear in Raman spectra, the polarizability of the molecule must change.  Polarizability transforms as x², y², z², xy, yz, or xz.  Examination of the basis functions for each of the vibrations in water show that each vibration will also be Raman active.  Thus, both the IR and Raman spectra will show the same three bands relating to vibration of the water molecule.
    For molecules with a center of inversion, there is an exclusion rule.  For molecules with a center of inversion, none of its modes can be both IR and Raman active.  As a result, the coincidence (or lack thereof) of vibration frequencies in the IR and Raman spectra can easily be used to determine if certain molecules are cis or trans.  For example, a square planar molecule of the general formula MX₂Y₂, can exist with cis or trans symmetry.  If the molecule exists as the trans isomer, it will posses a center of inversion, and hence bands which are seen in the IR spectrum of the molecule will not appear in the Raman spectrum.
 

Copyright ©1998 Beverly J. Volicer and Steven F. Tello, UMass Lowell.  You may freely edit these pages  for use in a non-profit, educational setting.  Please include this copyright notice on all pages.