|
|
example: [Mn(OH2)6]SO4 : coordination #=6, and sulfate is outer sphere.
[Mn(OH2)5SO4] : coordination # = 6, and sulfate is inner sphere.
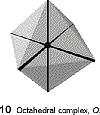
Coordination numbers can range from 2 up to 12, with 4 and 6 quite common for the upper transition metals. The following factors influence the coordination number of the complex.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
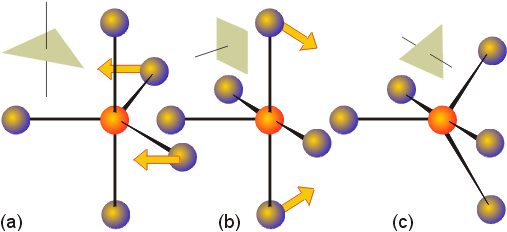
favored when metal is small and ligands are large |
 |
|
|
typical for d8 metals and complexes with p bonding ligands |
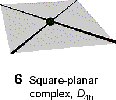 |
|
|
(square pyramid due to planar porphyrin rings) |
|
|
|
distortions include trigonal prism, especially for chelating ligands with a small bite angle |
 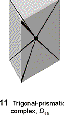 |
|
|
|
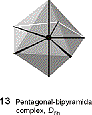 |
Certain coordination numbers, specifically 5 and 7, have several shapes which are similar in energy, with low energy barriers for inter conversion. An example of the fluctuating nature of these shapes can be seen in Berry pseudoratation of trigonal bipyramidal structures. The structure distorts in such a way that the axial groups become equatorial, with a square pyramidal structure as an intermediate.
The system of naming
inorganic complexes incorporates prefixes (mono, di, tri, etc.), to indicate
the number of ligands of each type coordinated to the metal. The
ligands have special names (and abbreviations). Typically, ligands
which are negatively charged end in o. A list of common ligands
is provided in the text on page 220. A common ligand which was omitted
are phosphines, and specifically triphenylphosphine, P(C6H5)3.
This ligand is often abbreviated as PPh3 or Pf3.
It is important to note that ligands such as this which have prefixes such
as di, tri, etc. in their names are enumerated using the prefixes bis,
tris and tetrakis when more than one of them is coordinated to a metal.
The format of naming
the complexes is as follows. Ligands are listed first in alphabetical
order (not including prefixes). This is followed by the name of the
metal, and the oxidation state of the metal in roman numerals in parenthesis.
prefix for ligands-ligand name-metal name-(oxidation state of metal)
An alternative system includes the charge on the complex (in arabic numerals) in parenthesis instead of the oxidation state of the metal. In addition, metal complexes which are negative in charge often use the latin root for the metal, and end in the suffix ate. The formula of the complex is always written in square brackets, with the metal appearing first, then negatively charged ions, and then neutral ligands. Ions which are outer sphere are written outside of the square brackets.
Multidentate Ligands (Chelating Agents)
Many ligands have
more than one site which can coordinate with a metal atom or ion.
These are referred to as ambidentate ligands. Small ligands
with two sites, such as NO2- (N or O) or SCN-
(S or N) can undergo linkage isomerism. The name of the ligand
indicates which site is bound to the metal. For NO2-,
the nitrogen linkage has the name nitro, and the oxygen linkage
has the name nitrito. For thiocyanate ion, the sulfur linkage
is named thiocyanato, and the nitrogen linkage is named isothiocyanato.
Larger ligands with
multiple bonding sites can bond to a single metal atom or ion at several
sites, forming rings. These ligands are referred to as polydentate,
and form chelate complexes. In the most stable situations, the chelating
agent will form 5 or 6 membered rings with the metal. This produces
the proper bite angle to produce octahedral symmetry around the
metal. In ligands with small bite angles, octahedrons will distort
to trigonal prismatic geometry.

One of the highly useful synthetic uses of chelating agents and metal ions involves the template effect, in which a group of ligands can be assembled by coordination to a central metal ion. A large variety of macrocyclic compounds can be synthesized in this way.
Isomerism and Chirality of Metal Complexes
There are several types of isomerism exhibited in transition metal complexes. In considering only complexes with octahedral geometry around the metal, the following types of isomerism are seen.
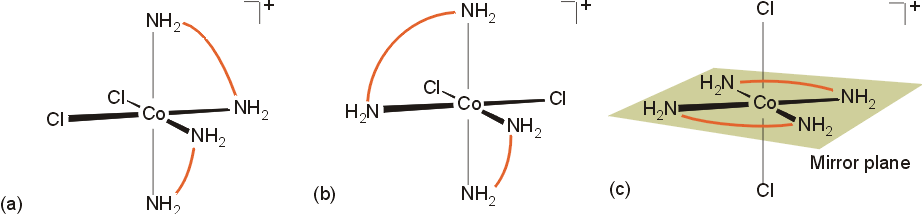
The violet product(s) are the isomers (a) and (b) above. They are mirror images of each other, and constitute an enantiomeric pair, cis - [CoCl2(en)2]+. The green product is isomer (c), trans-[CoCl2(en)2]+ which lacks optical activity. The yellow product, [Co(en)3]+, also exists as an enantiomeric pair. The three bidentate ligands can connect to the octahedral sites of the metal in a right handed or left handed fashion, similar to the blades on a propeller or the threads on a screw.
The isomers are designated with the greek symbols D (delta, for dextro) for the right handed complex, and L (lambda, for levo) for the left handed complex. Separation of enantiomers can be accomplished by reaction with a reagent with a chiral center. This produces molecules which have different solubilities, melting points, etc.
There are two widely used approaches to explaining the bonding and stability of transition metal complexes. Crystal Field Theory views the electronic field created by the ligand electron pairs surrounding the central metal as point negative charges which repel and interact with the d orbitals on the metal ion. This theory explains the splitting of the d orbitals to remove their degeneracy, the number of unpaired electrons in transition metal complexes, their color, spectra and magnetic properties.Return to Class Schedule
Bonding and Electronic Structure of d-Metal Complexes
Crystal Field Theory
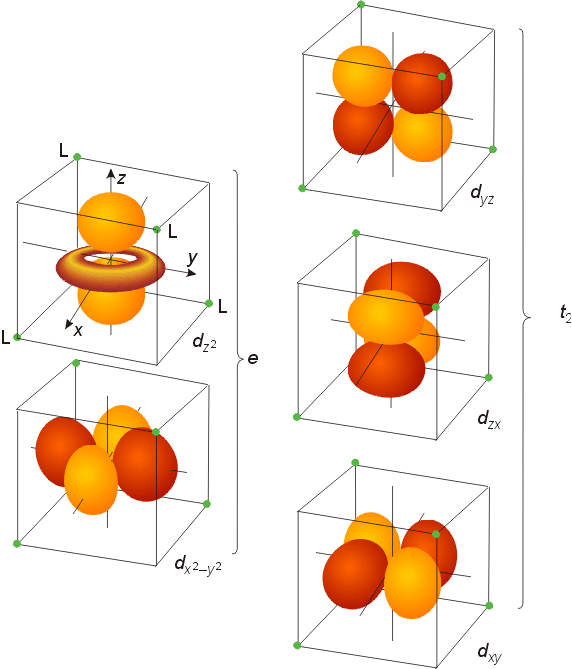
Examination of the spatial orientation of d orbitals shows that the dz2 and dx2-y2 orbitals point directly at the corners of on octahedron.Octahedral Complexes

The triply degenerate set has the symmetry designation t2g, and the doubly degenerate set has the designation eg. These designations are from the character table for the octahedral symmetry group, Oh. The magnitude of the splitting will depend on the metal and ligands involved. The size of the splitting is given the symbol Do, the ligand field splitting parameter, where the subscript o stands for octahedral. Since three orbitals are lower in energy and two orbitals are higher in energy than the original degenerate set, the energy is lowered by 2/5 Do for the t2g set, and raised in energy by 3/5 Do for the eg set. The magnitude of the splitting is determined experimentally from spectra of transition metal complexes. As the size of the gap changes, so does the color of the complex, as most of the t2g to eg transitions occur in the visible range.
As a general rule, the halogens are considered relatively weak ligands (a small value of Do ), water is somewhat intermediate in strength, ammonia is considerably stronger, and the strong p bonding ligands of cyanide and carbon monoxide are quite strong.I-<Br-<S2-<Cl-<NO31<N3-<F-<OH-<C2O42-<H2O<NCS-<CH3CN
<pyridine<NH3<en<bipy<phen<NO2-<PPh3<CN-<CO
The results of these trends is summarized in the list below. The smallest values of Do occur with the +2 ions, with increasing values observed for higher charged ions which are lower down in the table.
- Do increases with increasing oxidation number of the metal. This is due to the smaller size of the ion, resulting in smaller metal to ligand distances, and hence, a greater ligand field.
- Do increases as you go down a group. This is due to the better bonding ability of expanded shells using the 4d or 5d orbitals.
The relative values of the ligand field stabilization energy (LFSE) can be easily calculated in terms of Do . For each electron in the lower t2g set of orbitals, the complex is stabilized by a factor of 2/5 Do, or 0.40 Do . For each electron occupying the upper eg set of orbitals, the complex is destabilized bu a factor of 3/5 Do , or 0.60 Do . The LFSE for metals with d1, d2, or d3 electron configurations is unambiguous, and is equal to the number of electrons multiplied by (0.40 Do ). For 4 electrons, the size of the gap ( Do ) will determine whether the fourth electron enters the lower t2g set of orbitals, or the upper eg set of orbitals. The outcome will depend on the relative size of the splitting, versus the pairing energy. When the gap is relatively small, a weak field case arises, and the extra electron occupies the upper set of orbitals, rather than pair up with an electron in the lower set. When the size of Do is substantial, a strong field case results, and the gap is too great compared to the pairing energy, and the electron pairs up in the lower t2g set.Mn2+<Ni2+<Co2+<Fe2+<V2+<Fe3+<Co3+<Mn4+<Mo3+<Rh3+<Ru3+<Pd4+<Ir3+<Pt4+ Calculating the Ligand Field Stabilization Energy
The LFSE for the weak field case is equal to [ (3)( 0.40Do -(1)(0.60Do )] = 0.60Do . The LFSE for the strong field case is equal to (4) (0.40 Do ) = 1.6Do . The different electron configurations are referred to as high spin (for the weak field case) and low spin (for the strong field case). The possibility of high and low spin complexes exists for configurations d5-d7 as well. The following general trends can be used to predict whether a complex will be high or low spin.
- For 3d metals (d4-d7): In general, low spin complexes occur with very strong ligands, such as cyanide. High spin complexes are common with ligands which are low in the spectrochemical series, such as the halogen ions.
- For 4d and 5d metals (d4-d7): In general, the size of Do is greater than for 3d metals. As a result, complexes are typically low spin. Even a ligand such as chloride (quite weak) produces a large enough value of Do in the complex RuCl62- to produce a low spin, t2g4 configuration.
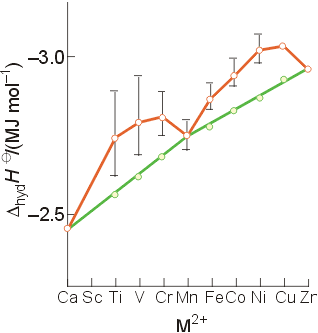
Evidence for LFSE can be seen in the enthalpies of hydration of the 3rd period M2+ ions. Without considering LFSE. the enthalpies should increase linearly as the size of the ion decreases and bond strength increases (the green line). Instead, the data show two "humps", with the enthalpies for the configurations d0, d5, and d10 falling in the straight line. The other metal ions show greater enthalpies of hydration (the orange line) in keeping with the calculated ligand-field stabilization energy for each configuration. When the calculated LFSE is subtracted from the observed values, they fall on the straight line which ignores LFSE, and only considers ionic size.
The Electronic Structure of Four-Coordinate
Complexes
Tetrahedral and Square Planar Shapes
The d orbitals of tetrahedral complexes also split into two groups. Examination of the symmetry tables shows that the dxy, dyz, and dxz have the same symmetry properties as the px, py, and pz orbitals. If the tetrahedron is viewed as ligands occupying the alternating corners of a cube, with the metal atom in the center, these d orbitals point in the direction of the ligands. As a result, they will be higher in energy than the degenerate orbitals of the free metal atom or ion. The dz2 and dx2-y2 orbitals point between the ligands (towards the center of each face of the cube), and are lower in energy.
The splitting pattern has the lower two orbitals (the eg set) stabilized by 3/5 DT , and the upper three orbitals (the t2 set) 2/5 DT greater in energy, where DT is the size of the splitting in a tetrahedral field. The size of DT is approximately half the size of the octahedral splitting Do for the same metal and ligands, so virtually all tetrahedral complexes are weak field/high spin.
Distortions of Octahedral Complexes
Octahedral complexes can undergo tetragonal distortions (the elongation of the z-axis, and shortening of the x and y axes) to become elongated into molecules with square planar (D4h) symmetry. This distortion is often observed in Cu2+ (d9) octahedral complexes. As the z-axis is elongated, the degeneracy between the dz2 and dx2 - y2 orbitals is broken, with the dz2 orbital lower in energy since the ligands are further away.
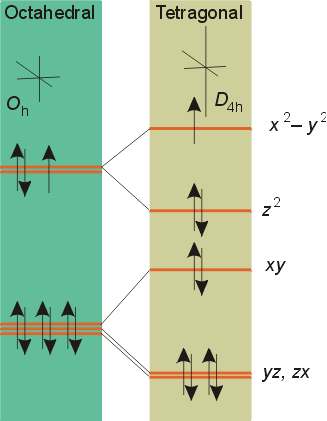
The extreme case of a tetragonal distortion is to form a true square planar complex in which the ligands along the z-axis are completely removed. In this case, the dz2 orbital drops even lower in energy, and the molecule has the following orbital splitting diagram.

As a result of these distortions, there is a net lowering of energy (an increase in the ligand field stabilization energy) for complexes in which the metal has a d7, d8, or d9 configurations, and thus electrons would occupy the upper eg set if an octahedral complex. In general, the size of the splitting in a square planar complex, DSP is 1.3 times greater than Do for complexes with the same metal and ligands. As a result, the distortion results in square planar complexes with lower energies than the comparable octahedral complex. This distortion to square planar complexes is especially prevalent for d8 configurations and elements in the 4th and 5th periods such as: Rh (I), Ir (I), Pt(II), Pd(III), and Au (III). Nickel (II) four-coordinate complexes are usually tetrahedral unless there is a very strong ligand fields such as in [Ni(CN)4]2-, which is square planar.
The Jahn-Teller Effect
The tetragonal distortions
described above are illustrations of the Jahn-Teller Effect.
The effect can be summarized by a statement which predicts which complexes
will undergo distortion. It does not predict the extent of the distortion.
|
If the ground electronic configuration of a non-linear complex is orbitally degenerate, the complex will distort so as to remove the degeneracy and achieve lower energy. |
Ligand Field Theory
An altnerative approach to understanding the bonding of transition metal complexes is Ligand Field Theory. Crystal Field Theory is a simple model which explains the spectra, thermochemical and magnetic data of many complexes. It's main flaw is that it treats the ligands as point charges or dipoles, and fails to consider the orbitals of the ligands. Ligand Field Theory applies molecular orbital theory and symmetry concerns to transition metal complexes. In octahedral symmetry, group theory can be used to determine the shapes and orientation of the orbitals on the metal and the ligands.
Examination of the
symmetry table for Oh shows that the orbitals on the
metal have the following attributes.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
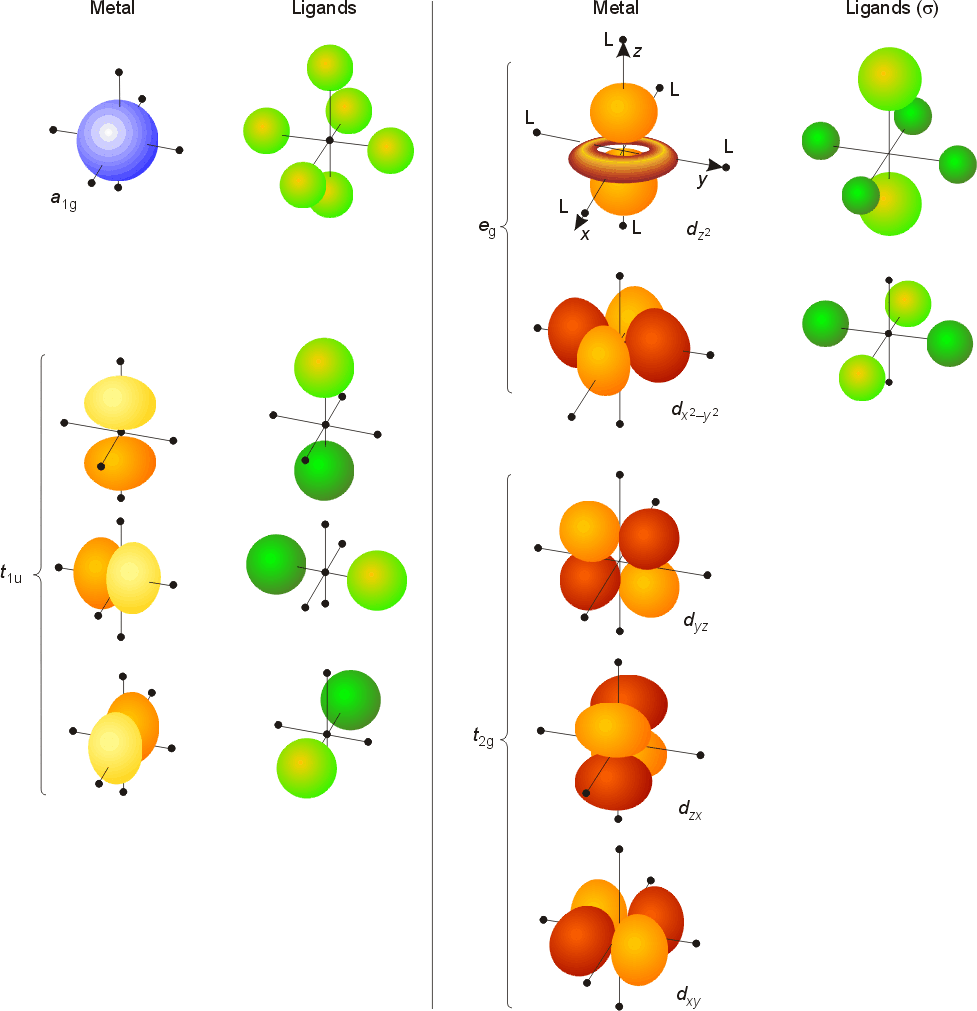
The t2g set (dxy, dyz, dxz) does not have any electron density along the bond axes, so these orbitals do not participate in sigma bonding, but will be involved with pi bonding. A molecular orbital diagram which estimates the energies of the bonding (show above) antibonding and non-bonding orbitals is shown below.
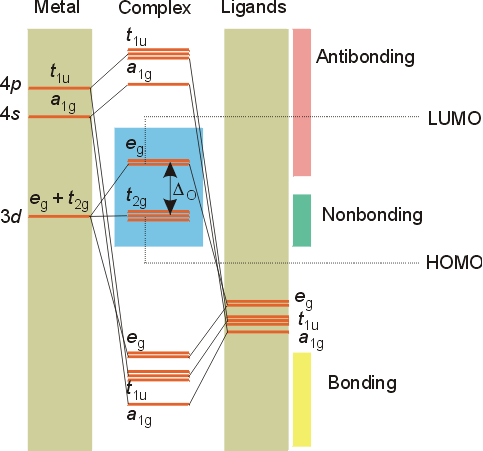
Since there is a large disparity in energy between the ligand orbitals and the metal orbitals, the lower lying molecular orbitals in the diagram are essentially ligand orbitals. That is, the electrons of the ligand lone pairs fill the lower levels (eg, t1u, and a1g). The d electrons on the metal will fill the t2g (non-bonding) and eg(antibonding) molecular orbitals. The split between the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) corresponds to the Do splitting in crystal field theory. In crystal field theory, the electrons in these orbitals are viewed as entirely on the metal atom or ion, whereas in ligand field theory the electrons are, to some extent, on the ligands, too.
pBonding
Pi bonding is not considered by crystal field theory, but is addressed in ligand field theory. The orbitals on the metal which were not used for sigma bonding (the t2g set: dxy, dyz, dxz) have the same symmetry properties as combinations of the p orbitals on the ligands. If the energy of the metal and ligand orbitals are comparable, the pi bonding orbitals formed will be significantly lower in energy thatn the atomic orbitals on either the metal or ligand. Likewise, the antibonding pi orbitals will be much higher in energy. If the orbitals are very different in energy, only slight mixing will occur. An example of pi overlap is shown below.
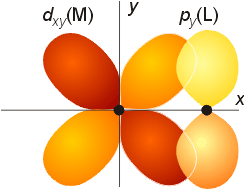
The effect on the molecular orbital diagram is as follows. The gap between the t2g and eg set will change, because the t2g set is involved in bonding, so there is not a bonding t2g set, and an antibonding t2g set of orbitals. The gap, represented as Do becomes the gap between the t2g set of antibonding orbitals and the eg set of orbitals. As a result, the size of Do dimishes.
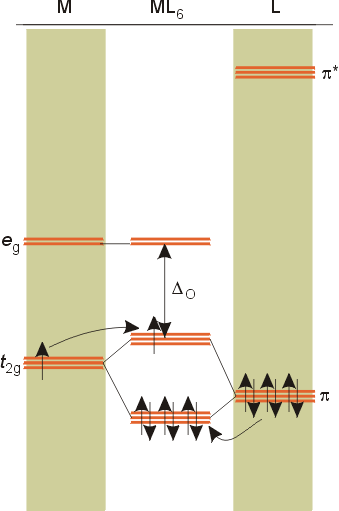
The above molecular orbital diagram is for ligands which have pi antibonding orbitals too high in energy to interact with the metal orbitals. The net effect for these pi donor ligands is to decrease the size of Do compared to ligands which only act as sigma donors.
Ligands may have empty pi antibonding orbitals higher in energy and with the same symmetry as the t2g orbitals of the metal. These ligands orbitals interact with the t2g orbitals of the metal creating a bonding orbital which is slightly lower in energy than the t2g set of the metal, and an antibonding set of orbitals which are much greater in energy than the eg set of the complex. The net result is that the size of the splitting, Do, increases, since the energy of the t2g bonding orbitals drops a bit.
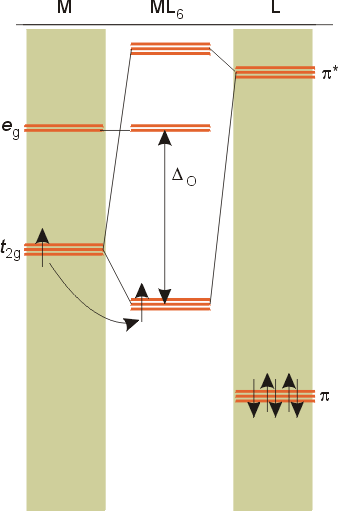
The net result is that pi acceptor ligands (such as CO and N2), with empty antibonding orbitals available to accept electrons from the metal, increase the size of Do. The spectrochemical series can be reconsidered with the possiblity of pi bonding in mind. It shows that the order (with some notable exceptions) goes as follows:
strong p
donor (small Do)
< weak p
donor < no p
effects (intermediate Do)<
p
acceptor (large Do)
The trend can be illustrated with the
following ligands as examples:
I-<Br-<Cl-<F-<H2O<NH3<PR3<CO,
CN-
Return
to Class Schedule
Copyright ©1998 Beverly J. Volicer and Steven F. Tello, UMass Lowell. You may freely edit these pages for use in a non-profit, educational setting. Please include this copyright notice on all pages.