Although it is relatively easy to predict the ground state electron configuration of an element, examining other possible configurations and how they might interact further complicates the picture.  Using a p² configuration (as in carbon) as an example, there are three major energy levels possible for the two electrons.  In addition, the lowest major level is further split into three slightly different energies due to spin-orbit coupling.  Spin-orbit coupling is a magnetic interaction which results when the spin and angular orbital momenta of individual electrons are strongly coupled together.
    The different energy levels of the electrons are designated using term symbols (or term states).  A term symbol consists of an upper case letter (S,P,D,F,G,H, etc.) which corresponds to the total orbital angular momentum quantum number, L, for the energy state.  The term symbol is preceded by a superscript which is the spin multiplicity of the configuration, and relates directly to the number of unpaired electrons in the energy state.  If spin-orbit coupling occurs, than a subscript follows the upper case letter.  The subscript is the value of J, the total angular momentum quantum number.  The process for determining term states and their relative energies will be illustrated with a p² configuration.

    The most systematic way to determine all the energy states for a particular electron configuration is to create a microstate table. The microstate table lists all of the possible arrangements of electrons for a specified configuration.  The table will show all the possible arrangements of electrons.  Once the table is completed, quantum numbers can be determined for the atom, rather than the individual electrons.  These atomic quantum numbers (L, S and J) are used to determine the term symbols for the atom.
    The quantum numbers that describe states of multi-electron atoms are:

L = total orbital angular momentum quantum number
S = total spin angular momentum quantum number
J = total angular momentum quantum number.

the possible values of L = l₁+l₂, l₁+l₂-1, l₁+l₂-2, .../l_1-l₂/ (L must be positive or 0))
the values of S = s₁+ s₂, s₁+ s₂-1, s₁+ s₂-2, ..../s_1- s₂/ (S must be positive or 0)

    For a p² configuration, the values of m_l for each electron can be 1, 0 and -1.  The value of L (the total orbital angular momentum quantum number) used to obtain the letter of the term symbol, can therefore range from a value of 2 (obtained from l₁+l₂) down to a minimum of 0 (obtained from /l₁-l₂/).  The The easiest way to determine all of the term symbols for the configuration is to use a microstate table.  The table will contain all the possible electron configurations of two electrons in a p subshell.  Note that configurations which violate the Pauli exclusion principle are not included in the table.  The table will include all possible electron configurations (called microstates) for all values of M_L (which range from 2 to -2 for a p² configurations) and all values of M_S (which range from 1 to -1 for two electrons).  Each microstate is represented by a number which is the l value of the orbital and a superscript + or - which indicates the value of m_s for the electron.  Thus, 1⁺1^- represents a pair of electrons in the p orbital which has a value of l equal to +1.  The electrons have opposite spins (indicated by the + and -), so they are paired.

    The microstate table can be used to determine the possible values of L and S, and the term states for a p² configuration.  For M_L =2, there is only one microstate in the M_S = 0 column.  This is the maximum value of M_L  in a series that ranges from +2 down to -2.  All microstates associated with this series are indicated in red in the above table.  The microstates indicated in red give rise to a term symbol or term state in which L=2, and S=0.  The term symbols which are generated by various values of L and S are summarized below:
 

L=	0	1	2	3	4
Term Symbol	S	P	D	F	G

   The term symbol for the red microstates in the table above will have a D designation, since L=2.  The spin multiplicity designation is equal to 2S+1, where S is the total of the spins for the electrons in an energy state.  For the red microstates in the table, S = 0, and the spin multiplicity is equal to 1.  The term symbol used to designate all of the red microstates in the table is ¹D.  This term is referred to as singlet D.
    Term symbols for the remaining microstates must also be assigned.  The microstates with the same term symbol will be grouped in a rectangular array, just as the ¹D microstates were.  There is a set of 9 microstates which are related to the same energy state and term symbol.  These are in a 3X3 rectangle which has M_L  = 1, 0 and -1, and the value of M_S = 1, 0 and -1.  These microstates are indicated in blue.  The term symbol for these microstates will be ³P, because the maximum value of L=1, and the maximum value of S=1.  This term is referred to as triplet P.
    There is one microstate that does not yet have a designation.  It is the one in the center of the table, O⁺O^-.  This microstate has an L=0, and S=0, so its term symbol is ¹S, or singlet S.  To summarize, the electron configuration p² has three major energy levels, designated as ³P, ¹D, and ¹S.

    Hund's rules can be used to determine which term state has the lowest energy.

1. The ground term has the highest spin multiplicity.  In the above example, the ground state term will be ³P.
2. If two or more terms have the same maximum multiplicity, the ground term is the one having the highest value of L.

    The more electrons in an atom or ion, the greater the number of microstates, energy states and term symbols generated.  For example, a d² electron configuration generates 45 microstates and term states of ¹S, ³P, ¹D, ³F and ¹G.  In general, you can look up the term states for a given configuration, rather than having to derive them.  However, it is quite simple to determine the ground term.  The ground term will have the highest spin multiplicity (maximum number of unpaired electrons) and the highest value of L (maximum values of M_L.  So, for a d² configuration, there will be two unpaired electrons, for a multiplicity of 3.  You can write out the orbitals and their values of ml to obtain the ground term value of L.  For d², the five orbitals have ml values of 2,1,0,-1 and -2.  Since the multiplicity rule requires that the electrons be unpaired in the ground term, the two electrons will have parallel spins in the orbitals with the two highest values of m_l.  The value of L will be 2 + 1, or 3, and the letter designation is F.  Thus, the ground state term for a d² configuration is ³F.

    The simplest configuration for a transition metal is d¹.  The ground level term state for the free ion will be ²D, because the multiplicity is 2(1/2) +1=2, for a single electron, and the maximum value of L=2, corresponding to a term symbol of D.  Because there can be no electron-electron repulsions or interactions, the level will split in an octahedral field, just like d orbitals split, into a T_2g (lower) level and an E_g (upper) level.  The term symbols for these new levels will still be doublets, because they could only contain a single unpaired electron.  As the strength of the ligand field increases, the magnitude of the splitting, D_o, increases.  This information can be summarized in a Correlation diagram, in which the free ion is shown on the left side, and the levels which result from the splitting in an octahedral field appear on the right side.

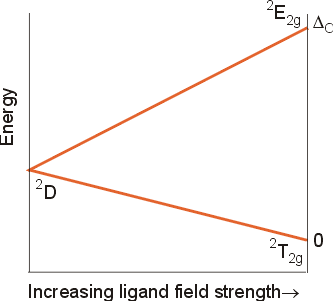
    Other energy states of the free ion will also split in an octahedral field.  In addition, the designations for the new energy states must have labels consistent with the symmetry of the point group (O_h).  The designations of the new energy states and their "parent" energy states are shown below.

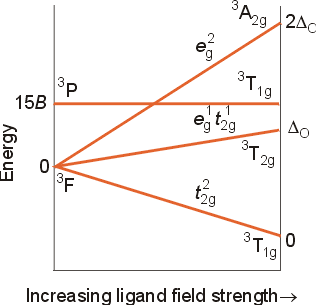
    The correlation diagrams for multi-electron configurations can be quite complicated, but are extremely useful in explaining the spectra of transition metal complexes.  For a d² configuration, the free ion has the following ground level energy state:  Maximum L= 2+1=3, so the letter designation is F, and the multiplicity will be 2(2/2) +1=3, for a term state of ³F.  The other term states arising from a d² configuration can be found in the text on table 11-5 (page 361).  The other terms are ³P, ¹S, ¹D, and ¹G.  A correlation diagram for this configuration is shown below.  Note that the free ion terms will split slightly in a weak field, and resolve into term states which correspond to recognizable electron configuration in an infinitely strong octahedral field.  The relative energies of the levels has been obtained using calculations and experimental data.  A few key features of the diagram should be pointed out.

    The notes at the far right side of the diagram show the electron configuration of the metal ion in an infinitely strong octahedral field.  The ground energy state of the ion in an infinitely strong octahedral field will be t_2g², because this would have two electrons in the lowest set of orbitals with parallel spins.  The next highest energy state would have the configuration t_2ge_g, representing one electron promoted to the higher, e_g set of orbitals.  the highest energy state would correspond to a configuration of e_g², with two electrons in the upper set of orbitals.
    In actual coordination complexes, the environment of the metal is intermediate between the free ion case and the infinitely strong ligand field.  As can be seen from the correlation diagram, each free-ion irreducible representation is matched with (correlates with) a strong-field irreducible representation having the same symmetry.  The different energies on the correlation diagrams relate to the absorption spectra of transition metal complexes.  Certain electronic transitions are favored over others, and the rules governing these transitions are called selection rules.

    The relative intensities of absorption bands are governed by a series of selection rules.  On the basis of symmetry and spin multiplicity of ground and excited electronic states, two of these rules are:

1. Transitions between states of the same parity (symmetry with respect to a center of inversion, i.e.,gerade or ungerade )are forbidden.  For example, transitions between d orbitals are forbidden (g->g transitions), but transitions between d and p orbitals are allowed (g->u).  This is know as the Laporte selection rule.
2. Transitions between states of different spin multiplicities are forbidden.  For example, transitions between ⁴A₂ and ⁴T₂ are "spin-allowed", but transitions between ⁴A₂ and ²A₂ are "spin-forbidden."

Tanabe-Sugano Diagrams

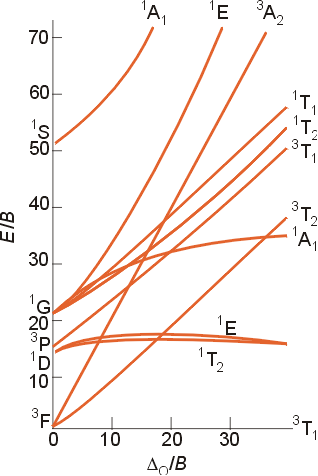
    Tanabe-Sugano diagrams are special correlation diagrams that are especially useful in the interpretation of the electronic spectra of coordination compounds.  In these diagrams, the lowest (ground state) energy state is plotted along the horizontal axis.  As a result, vertical distance above this axis is a measure of the energy above the ground state.  For the d² configuration, the ³T_1g energy state is the baseline of the horizontal axis.  The excited states are shown as well.  The quantities plotted in the Tanabe-Sugano diagrams are as follows:
 

• D_o/B :  where D_ois the octahedral ligand field splitting
• B : Racah parameter, a measure of the repulsion between terms of the same multiplicity.  For a d² configuration, the energy difference between ³F and ³P is 15B.
• E/B : where E is the energy (of excited states) above the ground state.

    Note that in the above diagram (as in many such diagrams) the subscripts (all g in this case) have been omitted for clarity.

    Below is the spectrum of the d³ complex [Cr(NH₃)₆]³⁺.  The two broad absorptions around 25,000 cm^-1 correspond to transitions involving electrons in the d orbitals.

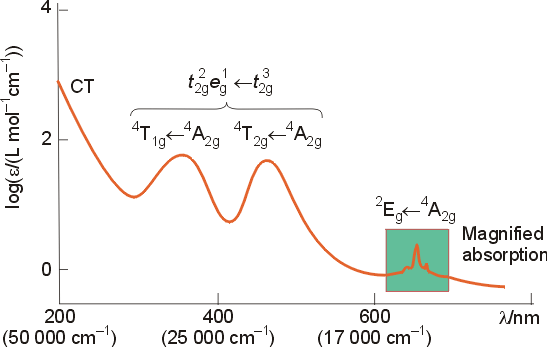
    The bands in the spectrum have been labeled, both with symmetry labels, and with electron configurations.  The two absorptions involving d to d transitions will be explained qualitatively, and then related to the Tanabe-Sugano diagram for a d³ configuration.  On a qualitative basis, it might seem like only one energy should be seen for a t_2g³ to t_2g²e_g¹ transition.  The splitting pattern for this complex is:

    Upon closer examination, it can be seen that transitions from the lower t_2g level to the higher e_g level are not all the same.  In the ground state, electrons occupy the d_xy, d_xz, and d_yz orbitals, and they will absorb energy and get promoted to either the d_z2 or d_x2_-y2 orbitals.  If promotion takes place from the d_xy to the d_z2 orbital, the transition shifts electron density from the xy plane to the high electron density z axis.  The z axis is rich in electron density because both the d_xz and d_yz orbitals, which contain an electron each, have electron density along the z direction.  This transition will result in an increase in electron repulsion.  An alternative transition could promote an electron from the d_xz to the d_z2 orbital.  This transition involves a small relocation of electron density, as the electron is already in an electron rich environment.   As a result, the two transitions discussed will have distinctly different energies.  In examining all the other combinations of transitions, there is either a large shift in electron density, or a small shift.  That is all transitions will fall into one of these categories, with three involving a large shift (from the d_xz and d_yz to the d_x2_-y2 ) and three involving a smaller shift ( the d_xy to the d_x2_-y2 , and the d_yz to the d_z2 ) in electron density.  The two types of transitions are illustrated below.  The type of transition shown in illustration (a) is from a low density area to a high density area.  The illustration (b) transition is between areas of more comparable electron densities.

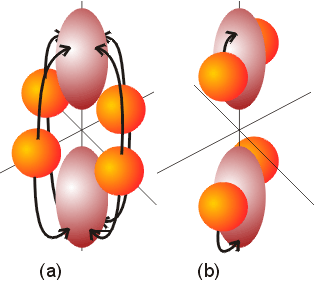
    Examination of the spectrum of the complex is consistent with this analysis, with two peaks of equal size in the region associated with  d to d transitions.
    The Tanabe-Sugano diagram for a d³ configuration is shown below.  The two arrows indicate the spin-allowed transitions which correspond to the analysis above and the two peaks shown in the region of the spectrum near 25,000 cm^-1.  The third spin-allowed transition from the ground state to the upper level ⁴T₁ is obscured by the strong charge transfer band in the spectum above. Note that the subscript g for gerade is left off for clarity.

    The ease with which D_o can be obtained from spectra depends upon the electron configuration of the metal and the clarity of the spectra.  Often bands are overlapping, and it is difficult to determine the true absorption peaks.  Assuming the spectra are resolved and absorptions are clearly defined, the configuration of the d electrons in the metal will dictate the ease with which the spectra can be interpreted.

    In each of these cases, the absorption spectra will result from the excitation of an electron from a t_2g orbital to an e_g orbital, with the excited electron configuration having the same spin multiplicity as the initial configuration.  In each case, there is a single excited state of the same spin multiplicity as the ground state.  As a result, there is a single spin-allowed absorption, with the energy of absorbed light equal to D_o .  Examples of these complexes include [Ti(H₂O)₆]³⁺, [Cr(H₂O)₆]³⁺, [Fe(H₂O)₆]²⁺, and [Cr(H₂O)₆]²⁺.  The spectra of these complexes show a single absorption band, with occasional splitting due to a Jahn-Teller distortion.

   These configurations have a ground state F term.  This term splits in an octahedral field into an A_2g, a T_2g and a T_1g term as illustrated in the Tanabe -Sugano diagram above to help explain the spectrum of  [Cr(NH₃)₆]³⁺, a d³ complex.  For a d³ or d⁸ configuration, the term of lowest energy is the A_2g.  The difference in energy between this term and the T_2g term (the next lowest energy state) is equal to D_o .  To obtain the value of D_o , you just need to determine the energy of the lowest energy transition in the absorption spectrum of the complex.  Additional examples of these types of complexes are [Cr(H₂O)₆]³⁺ and [Ni(H₂O)₆]²⁺.  For the complex [Cr(NH₃)₆]³⁺, the value of the lowest energy absorption is 21,550 cm^-1.  The hexaaqua complex has its lowest energy band at 17,500 cm^-1, indicating that ammonia produces a stronger ligand field than water for a given metal ion.

    The term for the free ion ground state is ³F, but the determination of the value of D_o is a bit more complicated than the previous cases.  The best way to interpret the spectra is to consult the appropriate Tanabe-Sugano diagram.

    The ground state for a d² configuration is ³T_1g, and there are three excited states with the same multiplicity ( ³T_2g and ³A_2g terms both arising for the free ion ground state F term and a ³T_1g term arising from the free ion P term).  Please note that the labels in your text and on the Tanabe - Sugano diagram above contain an error.  The triply degenerate state which arises from the P term is ³T_1g, and not ³T_2g.  The two terms of like symmetry, ³T_1g, may mix, and the result of mixing is that as the field strength increases, the states appear to repel each other, and the lines in the Tanabe-Sugano diagram curve away from each other.  As a result of the mixing of these states, and the subsequent curving of the ground energy state, the determination of the value of D_o is made more difficult.  The value of D_o is calculated using the ratios of the absorption frequencies in the visible spectrum of the complex.  This method will be illustrated in class.

    All d-d transitions are spin forbidden, and hence very weak.  Complexes of Mn²⁺ are colorless or faint pink (due to a spin-forbidden transition).

    The spectra of these complexes require a complicated analysis which will not be covered in this course.

    Transitions between the e  and t₂ orbitals are no longer Laporte forbidden, as the molecule doesn't have a center of symmetry.  As a result, absorptions may be more intense.  The electron configurations of tetrahedral complexes can be compared to those of octahedral complexes, and Tanabe-Sugano diagrams for octahedral complexes may be used to interpret the spectra of tetrahedral complexes.  For example, the arrangement of a single electron in an octahedral complex is the same as the arrangement of a missing electron (hole) in a d⁹ tetrahedral complex.

    Charge transfer spectra usually contain a very intense absorption in the ultraviolet or visible spectrum.  These transitions are both Laporte and spin allowed, and hence have extremely high intensity.  The transition can involve the transfer of an electron from molecular orbitals which are primarily on the ligands to a molecular orbital which is primarily on the metal.  This is known as a ligand to metal transfer (LMCT).   These occur when the ligand has lone pairs of relatively high energy and/or the metal has low lying empty orbitals.  Typical examples include metal ions which cannot have d to d transitions, such as Cd²⁺, Hg²⁺,  Fe³⁺, or Mn⁷⁺ and Cr⁶⁺.
    Electron transfer from the metal to the ligands is also possible.  In these cases (CTTL), the ligands typically have empty antibonding orbitals, such as CO, cyanide, SCN^1-and bipyridine.
 

Copyright ©1998 Beverly J. Volicer and Steven F. Tello, UMass Lowell.  You may freely edit these pages  for use in a non-profit, educational setting.  Please include this copyright notice on all pages.