
| Emilie and Paul attempt to find a general recursive rule for counting perfect matchings of hexagon snakes, while Jim, Martin, Sam, Abby, and Stephen watch. |
 |
 |
Paul takes stock of what we've just proved. |
| Carl and Brendan at work. |
 |
 |
Paul and Brendan try to figure something out. |
| The two formulas at the heart of our work on the Newton recurrence. |
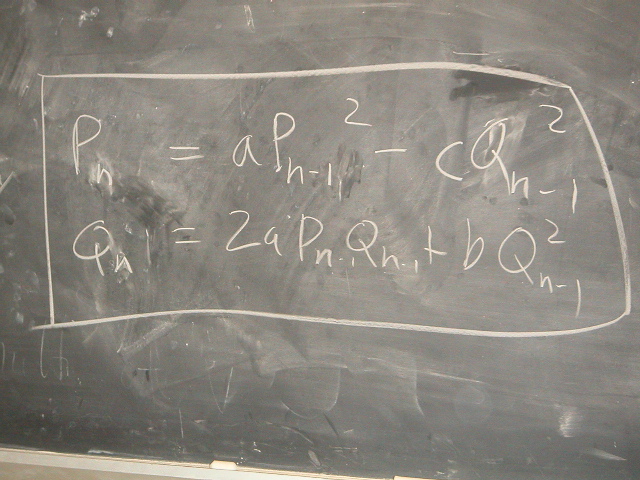 |
 |
Sam and Paul eat while pondering a double-sum relating to the Newton recurrence. |
| Carl and Sam get evidence from the computer. |
 |
 |
Paul and Emilie get the numbers they were hoping for. |