A bipartite graph is a graph whose vertices can be colored black
and red such that each edge connects a black vertex to a red one.
Given a bipartite graph that permits a perfect matching, one can think
of creating a matching of the graph by pairing every black
vertex with a red one. A perfect matching is a collection of edges
such that every vertex of the graph belongs to exactly one edge. An
example of a graph is shown in figure 1 on the left.
Many regular graphs that permit perfect matchings have interesting
properties. One way we can measure a property of a perfect matching
is to consider the probability that a given edge is in a random
perfect matching. The edge probability of edge E in graph
G is the number of perfect matchings of the graph obtained by
deleting E and both of its endpoints removed, divided by the
number of matchings of G itself.
One of the most fascinating region that has been studied is the
Aztec diamond. An Aztec diamond of order n is the union of unit
squares in the plane whose centers are contained in the equation |x| +
|y| <= n. The graph in figure 1 is an Aztec diamond of order 5.
Given a bipartite graph, one can convert the graph into its dual
tiling by dimers. A dimer is a shape consisting of two adjacent
faces, corresponding to two adjacent vertices in the matching. Each
dimer contains two faces where each face corresponds to a vertex in
the dual. Figure 1 shows a graph with a perfect matching overlaid on
its corresponding tiling on the right.
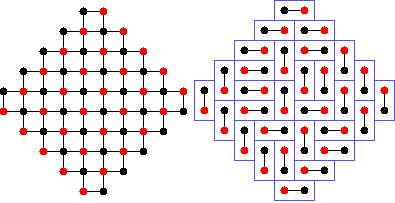
Figure 1
Order five Aztec diamond with a matching corresponding to a tiling
It is well known that a random tiling of an Aztec diamond has
non-homogeneous behavior, meaning that the probabilities of
corresponding edges indicating horizontal or vertical tiles, are not
the same if one moves from place to place in a matching. In figure 2,
which is a random tiling of an order 50 Aztec diamond, we can see the
varying behavior of the edge probabilities.

Figure 2
Random domino tiling of an order 50 Aztec diamond
1.2 Arctic regions
The tiling of the order 50 Aztec diamond as shown in figure 2 has
some interesting behavior near the four corners. It appears that the
tiling is actually not random at all, but really like all the tiles
are fixed in place; they are arranged in a simple periodic pattern.
The tiling contains a distinct boundary between the parts that appear
random and the part that looks uniform. This boundary is called the
Arctic boundary, whose name comes from the fact that everything
outside the Arctic boundary appears "frozen" in place. The behavior
of the tiling of an Aztec diamond is discussed in much more detail in [1].
The Aztec diamond is not the only region to have this Arctic
phenomenon. It is also true that hexagon tilings with lozenges have
this property. Hexagon tilings are discussed in much more detail in
[3]. We can see in figure 7, which is a random tiling of an
order 20 hexagon, that near the corners, all the tiles appear to be
fixed in place as in the Aztec diamond.
1.3 Pure phases
It is easy to imagine that given a tiling of a region, one can make
another tiling of the region by flip-flopping a small number of tiles.
For example on the Aztec diamond graph, it is possible to make another
tiling of the Aztec diamond by exchanging two horizontal dominoes for
two vertical dominoes given that the two dominoes form a 2x2 block.
If we go back to the dual matching picture, one can look at all the
cycles in the graph and consider those cycles that are alternating.
A cycle containing vertices {v1, v2, ...,
v2n} is alternating if there are exactly n edges
between consecutive vertices in the cycle. There are two ways of
having an alternating cycle. One way of having an alternating cycle
is to have v1, v2 matched; v3,
v4 matched, etc. The other way is to have v2,
v3 matched; v4, v5 matched, etc.
Thus given a perfect matching of a bipartite graph, we can create
another perfect matching, given that there exists an alternating
cycle, by replacing the cycle with its opposite. The result will be a
different perfect matching. An example of flipping a cycle is shown
in figure 3, which shows a 4-cycle being flipped in a domino tiling,
and then at the bottom showing how it relates to exchanging two
horizontal tiles with two vertical tiles in a 2x2 block.
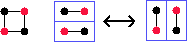
Figure 3
A cycle can be matched two ways.
A pure phase of a periodic infinite graph has the property that
there are no alternating cycles. We can see in the Aztec diamond
picture in figure 2, in the hexagon in figure 7, and in the fortress
in figure 10, that near the corners of the tilings, the tiles exist in
a pure phase, meaning that there are no local moves that can be made
there to produce another tiling.
With dominoes, it is possible to have two different pure phases
correspond to the same appearance of tiles. The tiles at the top and
the bottom of the Aztec diamond are both horizontal, but they are of
different pure phases. Since a domino corresponds to an edge in the
corresponding perfect matching, then it is possible to have a
horizontal domino with a red vertex on the left, and a different
domino with a black vertex on the left. Thus there are four different
types of dominoes, two types of verticals and two types of
horizontals. Figure 2 shows the four different types of tiles in four
different colors.
The Aztec diamond shows four pure phases, and with domino tilings,
these are the simplest pure phases. Other pure phases exist, such as
herringbone patterns, but these consist of a combination of the
simplest pure phases. You can see in figure 4 how a herringbone
pattern is just a combination of two simpler pure phases. Define the
set of simple pure phases to be the set of pure phases that are
independent of each other, so that one phase cannot be created from
other pure phases.

Figure 4
Herringbone pattern as a combination of two simple pure phases
It is not true in general, however that an arbitrary periodic
lattice will permit a pure phase. Figure 5 shows two counterexamples
of periodic semi-regular graphs that do not permit any pure phases.
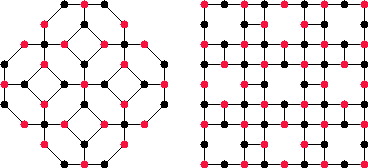
Figure 5
Two different lattices that do not permit a pure phase
2. Random Tilings
2.1 Creating Random Tilings
A random tiling is what one would obtain if he created all
the tilings of a region R, put them into a hat, and randomly
picked one out of the hat. Thus all the random tilings of R
have an equal probability of being chosen.
Except for very small regions, most interesting regions have so
many tilings that it would be completely infeasible to try to create
all of them, and then randomly choose one. For example, the order 50
Aztec diamond shown above has more tilings than particles in the
universe, so it would be impossible to make every tiling and then
choose one randomly.
The Propp-Wilson algorithm, as discussed in [4] is an
algorithm for creating a random tiling in a much more efficient way.
Since tilings of R exactly correspond to perfect matchings of their dual
graphs of R, it is easier to talk about creating a random
matching of a bipartite graph G. The Propp-Wilson algorithm
involves creating two special matchings and then coupling them
together to make a random matching.
Before, we talked about flipping cycles to make different
matchings. An alternating cycle can have two states, called the
minimum and maximum states. An alternating cycle is in its
minimum state if while one looks at the vertices in a clockwise order,
then for each edge in the cycle, the black vertex occur before the red
one. The cycle is in the maximum state if the red vertex comes before
the black vertex. Figure 3 shows a cycle in the graph, along with its
minimum and maximum states in a matching. A cycle can be
raised or lowered by moving it between its minimum and
maximum state. This definition for raising and lowering cycles is
arbitrary and the opposite definition is also perfectly equally
valid, but it just needs to be consistent.
It is possible now to make a minimum matching of a whole
graph simply by flipping all existing alternating cycles to their
minimum state so that no maximum alternating cycles still exist. For
a finite region, there is always a finite number of lowering moves
that need to be made until it is impossible to make any more. It is
also true that the minimum matching of any region is unique. The
maximum matching is made the same way as the minimum matching,
but is made by raising all the cycles until there is no cycle that can
be raised. For the Aztec diamond, the minimum matching contains only
horizontal tiles and the maximum matching contains only vertical tiles.
The Propp-Wilson algorithm involves making two matchings of the
same graph become more like each other until they became the same.
During each time step, look at all the cycles in both matchings, and
if there is a cycle that is flippable in both matchings in the same
location, flip a coin, and make the cycle at the minimum state in both
matchings if the coin comes up heads, and maximum otherwise. This
way, the matchings become more like each other because a discrepancy
at a particular cycle will be removed. Two matchings have
coupled if they have become the same as a result of removing
discrepancies. If a particular cycle is alternating in only one of
the matchings, matchings, then set only that cycle according to the
coin flip.
To start the Propp-Wilson algorithm, create the minimum and maximum
matchings of the graph. These are the two special matchings that were
mentioned before. To make a random matching, we use a "coupling from
the past" method that goes as follows: Start at some time -t and
evolve the matchings for t time steps. If they have coupled at
time zero, then the coupled matching is random. If they have not
coupled, then start at time -2t, and run until time zero, but
using the same coin flips between -t and 0, as before.
If they still have not coupled after 2t time steps, start at
time -4t and run for 4t time steps until hitting time
zero, but making sure the same coin flips are used between time
2t and 0. We repeat this process, starting from -8t,
-16t, and so on as necessary.
It is important to use the "coupling from the past" technique when
creating a random tiling, and not to just start with the minimum and
maximum at time 0, and evolve them until they couple. Using this
alternate technique will result in a biased result and some matchings
of G will occur more frequently than other matchings, thus
making the random matching not uniformly random.
2.2 Vaxrandom
In order to create random matchings of bipartite graphs in
practice, we have written computer software to run the Propp-Wilson
algorithm. However, just starting with a bipartite graph is not
enough to make a random matching. The Propp-Wilson algorithm requires
that we have a sample matching of the graph from which we can compute
the minimum matching by lowering cycles and the maximum matching by
raising cycles.
A newly written program called vaxrandom.c accomplishes all of
these things. It first reads in a file representing a graph, and then
it runs a max-flow algorithm to either come up with a perfect matching
of the graph or demonstrate that the graph does not permit a perfect
matching. Once the program has a sample matching, it determines where
all of the cycles in the graph are, so that it can raise and lower
them. Vaxrandom proceeds by doing as many raising and lowering moves
are necessary to make the maximum and minimum matchings. Finally, it
runs the Propp-Wilson algorithm by coupling from the past to actually
create a random matching.
2.3 The Arctic Region
We can define the Arctic region of a matching more precisely now.
It is true that it shows a group of tiles where no local raising or
lowering moves can be made, but more precisely, the Arctic
region of a matching is the largest set of edges of the matching
that exactly match the corresponding edges in either the minimum or
the maximum matching, that contains no islands in the middle.
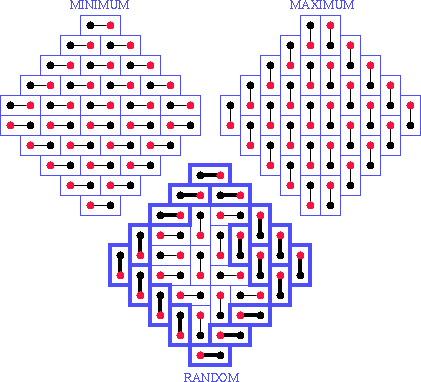
Figure 6
Maximum and minimum matchings defining Arctic
region on random matching (same one as in fig 1)
Figure 6 illustrates an order five Aztec diamond matching, along
with its minimum and maximum, highlighting the edges that are in the
Arctic region.
One property of the Arctic region of a graph that does not contain
any forced edges is that it consists of several distinct chunks all
touching each other at a single point on the boundary of the region,
and the chunks are pieces of the simple pure phases of the graph. We
can see in the Aztec diamond that all four pure phases appear with the
two from the minimum at the top and bottom and the two from the
maximum at the left and right sides.
3. What is Known about Arctic Regions
3.1 Aztec-like boundaries
It has been proved in [1] that the shape of the arctic boundary of
an Aztec diamond approaches a circle in the limit as the order grows
to infinity. It is also true that for a hexagon tiled with lozenges
that it also has a circular Arctic region. Figure 7 shows an order 20
hexagon.

Figure 7
Random tiling of an order 20 hexagon
The fact that both Aztec diamonds and hexagons have circular Arctic
boundaries suggests that it is possible that other regions should also
have Arctic circles. However, some regions do not even have Arctic
regions. A domino tiling of a 2n x 2n square has
homogeneous behavior everywhere through the tiling showing it is an
example of a region with no "frozen" areas. In the limit as n
grows to infinity, the probability of seeing any of the four types of
dominoes in any location approaches exactly 1/4.
The main question now is when does a region have an Arctic
boundary, and if it does, then is the boundary circular? If not, what
shape is it?
One important similarity between the Aztec diamond and the hexagon
that is not present in the square is that if one traverses the
boundary of the matching, the colors of the outermost vertices stay
the same for a long stretch, and then change once, but then stay the
same again for the next stretch. Figure 1 shows how the Aztec diamond
has all black vertices along the upper left and lower right sides, and
all red vertices along the upper right and lower left sides. This
property is also true of hexagons, but not for squares. We define
a boundary having this property an Aztec-like boundary. Along
each side of the square, the outermost vertices alternate between red
and black and do not stay the same color, so the boundary is not
Aztec-like.
One conjecture I present here is that any region with an
Aztec-like boundary will illustrate an Arctic region. It is intuitive
to see that if a tile near the corner of a region with an Aztec-like
boundary is oriented a certain way, then many tiles are forced as a
result. Figure 8 shows how this is true for an Aztec diamond and a
hexagon. Putting the yellow edge where it is forces the placement of
all the blue edges. Because of the large amount of forcing, it would
be highly unlikely for an edge equivalent to the yellow one to appear
in a random matching.
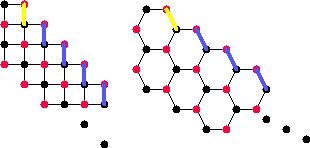
Figure 8
How edges get forced along an Aztec-like boundary
3.2 Arctic regions of Other Regions
We have seen two examples of regions with circular Arctic regions,
but are there other regions with Arctic circles? The square grid and
hexagon grid are the only two perfectly periodic graphs that are
bipartite. They are bipartite since all of the cycles have an even
length. The triangle lattice is the only other perfectly periodic
lattice in the plane, but since its cycles are of order 3 and 3 is
odd, then one cannot make a bipartite graph from the triangle lattice.
We saw that in both the Aztec diamond and the hexagon that all of
the pure phases are present in a random tiling as the order grows
larger. A second conjecture I make here is that every region with an
Aztec-like boundary will exhibit all of the pure phases of the
underlying lattice.
The simplest non-regular lattice with the most regularity in the
plane that is bipartite is the square-octagon lattice. One can define
a region of the lattice called a fortress that has an
Aztec-like boundary. Figure 9 shows an order 5 fortress graph, with
its matching and dual tiling overlaid. The fortress has an Aztec-like
boundary will all black vertices at the outermost edge on the upper
left and lower right sides, and red vertices on the outermost edge on
the other two sides.
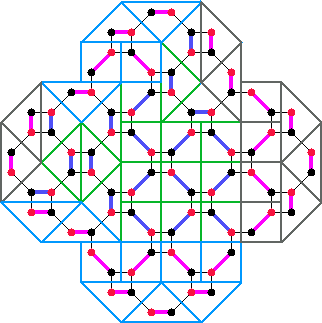
Figure 9
Random tiling of an order 5 fortress
Figure 9 shows many things about a fortress tiling. It shows how
it is generated from a square-octagon lattice. The blue and purple
edges are the edges in the matching, with the purple ones being in the
Arctic region. The dimers used to make the tiling are either
triangles or squares depending on how they fit in the matching. There
are four clumps in the Arctic region as shown by the dimers being
accentuated. The clump at the top and the one at the bottom are
highlighted in blue tiles and the eastern and western clumps are in
gray tiles. The tiles in the middle that are not part of the Arctic
region are indicated in green.
Fortress tilings show four pure phases which are all just rotations
of each other, as with domino tilings. In fortress tilings, a pure
phase consists of distinct rows that alternate between triangles and
squares. We can see at the bottom of figure 9 part of a pure phase in
blue tiles. Figure 10 shows an order 25 fortress, showing larger
Arctic regions. The four chunks are the four different types of pure
phases.

Figure 10
An order 25 fortress
4. What is Currently Not Known Yet
It is true that the simplest region with an Aztec-like boundary
yields an Arctic circle for every grid that is perfectly regular.
There are only two examples which are the square and hexagonal grid,
and regions on both of these lattices have circular Arctic regions.
It is now possible with vaxrandom to produce random tilings of
more general regions so that we can generate large samples of fortresses
and other regions to see what the shape of their Arctic regions are.
We have shown empirically that fortresses do not have circular Arctic
regions. Figure 10 shows an order 25 fortress tiling with its Arctic
region accentuated. The four Arctic chunks are highlighted in
different colors.
A striking difference between Aztec diamonds and fortresses is the
amount of time that is necessary to produce a random tiling. It has
been shown experimentally that Aztec diamonds couple in approximately
O(n^4) time where n is the order of the Aztec diamond. It is feasible
to produce random tilings of large Aztec diamonds of order 100 or
greater so that the Arctic boundary is much easier to see. However,
fortresses do not appear to couple in O(n^4) time. It is possible
that they do not even couple in polynomial time, or if they do, it
might be O(n^8) time or longer.
It has not been proven, but it makes sense that the main reason for
the long coupling time with fortresses is their large cycles. For the
Propp-Wilson algorithm to make two matchings become more like each
other, a cycle must be alternating at the same place in both matchings
that are coupling. For an octagon, which is an 8-cycle, it is a lot
less likely to be alternating than a 4-cycle as in the Aztec diamond.
What else is important is that not all the cycles in the fortress grid
are of the same length. Half of the cycles in the fortress graph are
8-cycles and the rest are 4-cycles. It is possible that since the
4-cycles are so much more likely to flip than the 8-cycles that the
8-cycles do not get flipped often enough by the Propp-Wilson
algorithm.
Since it is infeasible to generate a large random fortress tiling,
it is much harder to determine the shape of its Arctic boundary. We
can see an approximation in figure 10, though.
It is possible to make many different types of regions with an
Aztec-like boundary based on a semi-regular lattice, and all of them
yield an Arctic region. The Aztec diamond, hexagon, and fortress are
three examples, but there are many others. In fact, I conjecture that
the intersection of an Aztec diamond graph and any periodic matching
on the square grid, without holes, will produce a region with an Arctic
region that converges to an asymptotic shape as the order of the Aztec
diamond increases to infinity. One interesting example of this is
shown in figure 11. On the left is a picture of a small graph with a
simple repeating grid, and on the right is a tiling of an order 30
Aztec diamond tiled with that particular lattice known as the dragon
lattice. Note that there are a few forced edges on the matching on
the lower left side. We can see here that there are six different
pure phases, all highlighted in different colors, and in fact these
six pure phases are all six possible pure phases for the dragon
lattice.
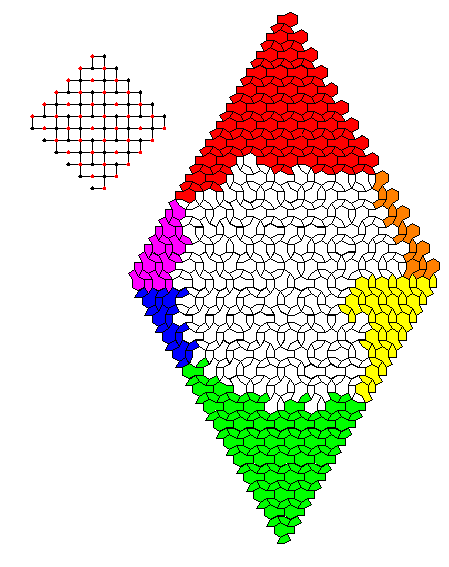
Figure 11
An order 30 dragon
5. Conclusion
Random tilings show many different and interesting features,
including pure phases and Arctic regions. It is striking to see how a
random tiling has non-homogeneous behavior and how near the corners of
the tiling, the tiles do not appear random at all. We have seen three
distinct examples of this behavior.
Even though it is known and has been proved that the shape of the
Arctic boundary is a circle for the Aztec diamond and the hexagon, it
is not known for more general regions. However, just recently,
a method called generalized shuffling has been developed, which allows
one to find quickly the probabilities of all of the edges in a graph
which is a subset of the Aztec diamond. Generalized shuffling is
mentioned in [1] and [4] in more detail. Most bipartite graphs can be
deformed to fit inside an Aztec diamond, thus allowing us to use the
same algorithm to find edge probabilities of more general regions.
The edge probabilities for the Aztec diamond and hexagon have been
known for a long time, and the shape of the Arctic region has been
known. Now, with the knowledge of the edge probabilities for more
general graphs such as the fortress, it may become possible to
determine the shape of the fortress Arctic boundary using shuffling.
Shuffling can also be used to find a random perfect matching of a
subset of the Aztec diamond graph very quickly. It is described more
in [2]. This algorithm is quite valuable in empirically showing the
behavior of the Arctic regions of tilings. The slowness of the
Propp-Wilson algorithm limits us to fortresses of about order 40, but
we can go up to about order 250 for fortresses now with shuffling.
The main constraint becomes space instead of time.
Although much information about random tilings is unknown at this
time, we are rapidly gaining knowledge about them. A possible next
step would be to describe the shape of the Arctic boundary for
matchings of much more general regions, and then to possibly describe
behavior in the interior of such regions.
References
[1] Jockusch, W., Propp, J.,, Shor, P., "Random Domino Tilings and
the Arctic Circle Theorem", October 10, 1995.
[2] Wilson, D., and Propp, J. "How to Get a Perfectly Random Sample
From a Generic Markov Chain and Generate a Random Spanning Tree of
a Directed Graph", May 21, 1997.
[3] Cohn, H., Larsen, M., Propp, J., "The Shape of a Typical Boxed
Plane Partition", September 2, 1996.
[4] Propp, J., Wilson, D., "Exact Sampling with Coupled Markov
Chains and Applications to Statistical Mechanics",
Random Structures and Algorithms. Vol. 9, pp. 223-252, 1996.










