SSL Minutes
1 Feb 2001
Hal and Geir
Jim Propp Talks about SSL.
Each individual is expected to create something (code, illustrations, documents, proofs).
Slogan: ``Teach what you know, learn what you don't, document everything.''
Grant Proposal.
Somebody is in charge of keeping the Glossary.
Disseminate everything on the web.
Shared Bonuses. For example, Prove the Baxter Permutation Conjecture for an hour's extra pay (for everybody).
Earn an extra hour's wages by attending Combinatorics Seminar 2:25-3:15 M 903 VV (next week only)
Get Time Cards. 2nd floor VV. Hand it to Propp or put it in his mailbox. Today counts as work.
We can spend money on supplies, for example, books. We have a LaTeX book somewhere.
Homework #1: Count the number of Domino tilings for 2xN rectangle, for n<=10. There is a pattern there. Find it and exploit it.
Public Web Site: http://jamespropp.org/SSL/ There is a private web site and an email list.
Accounts on dodgeson will be done on Thursday.
Mathematics:
We know some things about an Aztec Diamond. But what about a rectangle or square?
The number of domino tilings of a 2n-by-2n square is:
\begin{displaymath} \product_{j=1}^n \product_{k=1}^n (4 \cos^2 \frac{\pi j}{2n+1} + 4 \cos^2 \frac{\pi k}{2n+1}) \end{displaymath}
Is it an integer? Yes: you can use Galois theory to show that it's a rational number and algebraic number theory to show that it's an "algebraic integer". The only numbers that are both rational and algebraic integers are integers.
To prove that something is an integer: (1) Cook up a combinatorial problem it describes (2) Reverse engineer the algebra.
A different kind of tiling problem.
Domino vs. Lozenge tilings: (Fig 1 and 2)
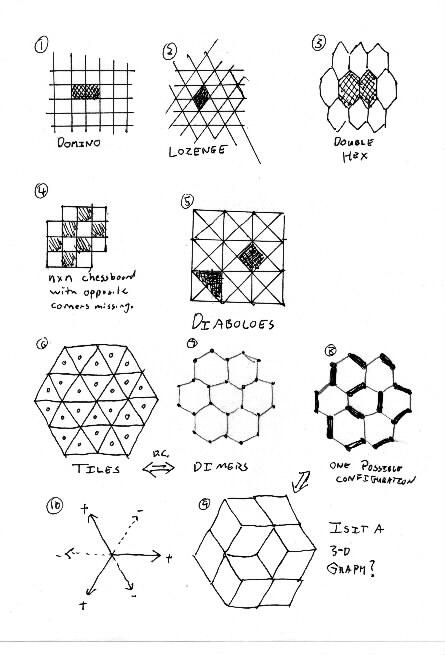
Dominos are 1x2 rectangles in a grid. Lozenges are two touching equilateral triangles.
Double-Hexes (Fig 3) don't do anything cool, because they don't have height functions.
Not all areas are tilable: Hal asks about the nxn chessboard missing two opposite corners. (Fig 4)
Also look at Diaboloes; (fig 5) they are also interesting.
One can color tiles alternating colors if each vertex has an even number of cells touching it.
Not going to talk about dual graphs. ``The dual graph is bipartite.''
The Dimer Problem.
Look at the dual correspondence between tiles and Dimers in figures 6 and 7. In Fig 6, we need to connect triangles that share edges to form lozenges.
In Figure 7, we need to find a dimer configuration such that each vertex is paired with exactly one neighbor.
Pick a random configuration: notice that once you make a few decisions, others are forced upon you. (Fig 8)
Now convert it back to lozenge tilings. Suddenly, we see a 3-d cube figure! (Fig 9) Figure 10 shows positive and negative directions.
Now Boytcho produces a double die so that we can see a cube within a cube.
Let height be defined as h(x,y,z) = x + y + z
Figure 11 shows the height of each vertex.
Figure 1 shows Abe's 2-d analog, so we understand what height really means. In this figure, the line x+y=0 represents height=0. The point (1,2) has height=3. Its ``real'' distance from the h=0 line is 3/\sqrt{2}. But we like integers!
Now we need to mathematically define a way to calculate what your eye sees as height.
Height
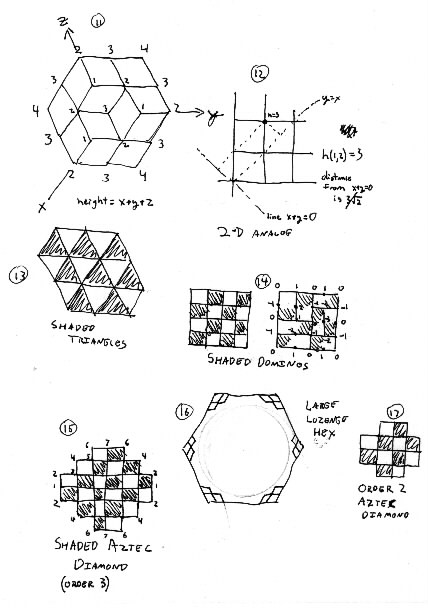
Imagine moving along the edges of the shaded triangles of figure 13. If it is shaded on your left, increment your height by one. If it is unshaded on your left, decrement your height by one.
This way we generalize what a height function is. We can define the height of a vertex on a domino graph by analogy to lozenges. (Fig 14)
On a square, the boundaries must be alternating zeros and ones on top and bottom, and alternating zeros and minus ones on left and right. Boring.
But on an Aztec Diamond of order 3, the height goes up from 1 to 7 as we go from left to top, then back down and up as we go around the other sides. (Fig 15) These different boundary conditions change how the inside behaves. The Aztec diamond is approximately a saddle shaped surface. That's why the corners freeze out.
You can think of a large lozenge hexagon as a monkey saddle. All six corners freeze out, leaving a circular area, like figure 16.
Assignment:
(1) Count the number of Domino tilings for 2xN rectangle, for n<=10. There is a pattern there. Find it and exploit it.
(2) Find all domino tilings of Aztec Diamond of Order 2.
See figure 17. Find all height functions. Look at several
Order 3 Aztec Diamonds, with height functions. Try to figure
out what heights can occur at the different vertices of an
Order 3 Aztec Diamond.