SSL Minutes
13 Feb 2001
Rachel
Jim asked us what we plan to do after graduation. Most of us plan to go to graduate school at some point in our lifetime.
Then we went over our homework. Pavle gave a cool algebraic proof for our first problem, that Jim noted was a telescoping sum and further simplified.
Domino Shuffling and Hexagon Matchings
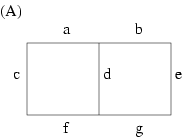 There was a longer discussion over our second problem, using domino
shuffling to prove that H(2,2,2,) = 20. The claim in the paper is, in
order to count perfect matchings of these tiled hexagons, first "flatten"
them into square grids, and then count. Give each matchings weights for
example, for this graph (Figure A) we have cde + aef + bcg. Give weights
of zeroes and ones, with zeroes to the vertical edges so that they don't
contribute to the sum.
There was a longer discussion over our second problem, using domino
shuffling to prove that H(2,2,2,) = 20. The claim in the paper is, in
order to count perfect matchings of these tiled hexagons, first "flatten"
them into square grids, and then count. Give each matchings weights for
example, for this graph (Figure A) we have cde + aef + bcg. Give weights
of zeroes and ones, with zeroes to the vertical edges so that they don't
contribute to the sum.
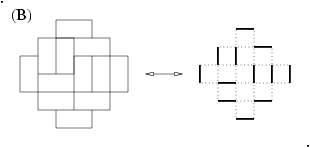 Boytcho had a question about how do we fit these flattened hexagons into an
Aztec diamond graph? NOTE: there IS a difference between an Aztec diamond
and an Aztec diamond graph! (my name is gecko, not to be confused with
geico, which can save....) See Figure B as an example to differentiate
between the two.
Boytcho had a question about how do we fit these flattened hexagons into an
Aztec diamond graph? NOTE: there IS a difference between an Aztec diamond
and an Aztec diamond graph! (my name is gecko, not to be confused with
geico, which can save....) See Figure B as an example to differentiate
between the two.
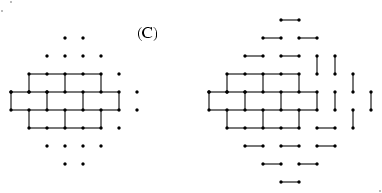
Boytcho's question further asked, what weights would you assign to the
flattened hexagons when trying to fit them into the Aztec diamond
graph? Jim showed examples where it does and where it does not work to fit
them in. Basically you must match the inner graph with the outer
graph. See Figures C1 (not able to fit it into an Aztec diamond graph of
order 4) and C2 (are able to fit it into an Aztec diamond graph of order
5). In C2, where the fitting DOES work, note the matchings that were NOT
forced; there are only four possibilities between these, hence the
"conclusion: the sum of the weights of the matchings of the graph is equal
to four times H(2,2,2,)".
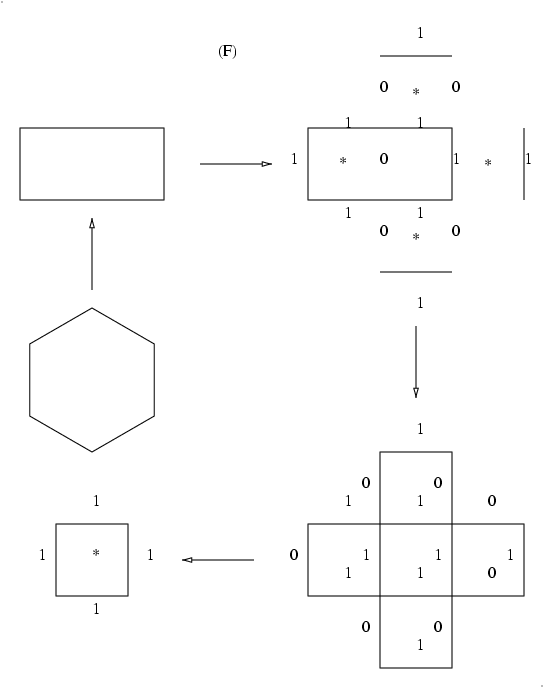
Jim explained and gave two examples of the reduction algorithm. This
algorithm is shown in the domino-shuffling handout, but Figures D1 and D2
show the step-by-step process of the examples that Jim explained. The
second example is with a simple crushed hexagon to aid us with our
homework. The basic procedure is to star every other cell, switch opposite
weights on each cell, divide by the cell factors, erase the outer edges and
then start the procedure over again. Finally you multiply all the cell
factors and voila!; you wind up with the number of perfect matchings of the
original graph.
We ended our session with Jim asking about a previous homework assignment,
basically that we find questions and ideas about the Project Summary
handout. We went around in a circle and these are the questions we listed
(the questions that Jim answered have answers succeeding in square
brackets, other questions to be answered in the future!):
What should we do?
"What should we do?" [Read Sections 1, 2, 3, 4 of the generalized shuffling handout; read the entirety of the grant proposal; start programming if you can, programming neophytes should work on manual calculations; think about what other types of programs we want or need?]
Ergodic theory?
Positive and zero entropy regimes?
Will non-programmers be able to contribute? To whom can they talk? ['Computer mentors' such as Abe, Hal, Boytcho; also we can use our funding to purchase reference books for example, for programming.]
Pfaffian method?
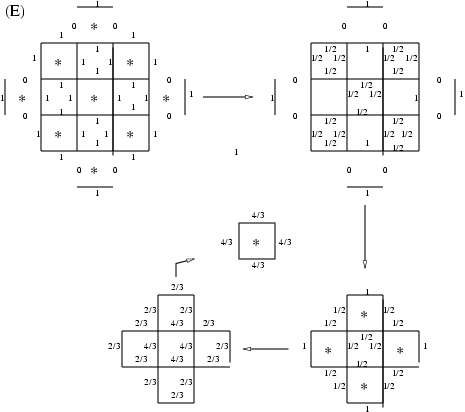
When do we start? [Now! See Figure E and think about patterns, in this theoretical example and in examples of your own. In programming/coding, look for patterns!]
Aztec circle?
Role of wild ideas?
What should Hal program? (What should we program?)
Finally for all you vegetarians out there, Jim noted that cochineal extract is extracted from bugs, so if you plan to be a pure vegetarian, it is recommended to look for mosquito extract on fruit juice ingredients listings before you partake! (Thanks so much! Someday I will have so many things on my list of what NOT to eat that I will just constantly be spooning up tofu! How exciting!)