SSL Minutes

SSL Minutes

20 Feb 2001
Hal and Nick

Misc.

We were missing a couple of SSLers including Rachel, who was supposed to bring brownies. And we had a new guy, Joel. Hi, Joel.
There will be an "open bar" in the hallway on Thursday. We will drink up the excess beverages.
Clarification of previous notes:
Original: "maximum entropy is found at very center of Aztec Diamond"
Revised: there may be "bad spots" near center, but they'd be small enough to be negligible.
Why: Entropy is a statistical property, and we look at a small statistical region at the center of the diamond. If there is a bad spot, it is *statistically* small. Is that clear enough while still being accurate?
On Thursday, everyone will meet individually for 10-minute with Prof. Propp and Mike. A schedule has been devised. In the other room, we get to play on the computers and Abe will talk about *nix OSes and programming, the Hal will talk about his program.
Is everyone caught up on reading? Hal is not. Jim said that that can be a good thing, as long as you ware working on something else and asking good questions. For example, the "tilability question," or Boytcho's "Is there an analog to domino shuffling for diabolo tiling of a fortress?"
What are sticky points on the reading? "Why Generalized Domino Shuffling called GDS?" Also, someone asked about the notation in one of the papers.
ASMs and Domino Tilings

A domino tiling of an AD can be described with a height function and put into a matrix.
      N          nN     nN = a north pointing domino
     E N        wEnN  
    W E E  ==  wWeEwE   Ss = a south pointing domino
   W N W       WnNeWe 
    S S         SsSs    E  = a east pointing domino
     S           Ss     e

                        w  = a west pointing domino
                        W
In this picture, capitol letters represent black squares on a chess board and lowercase letters represent white squares. Obviously it is only necessary to enumerate which domino is the black tiles.
This is how Hal's been thinking about it, because that's how his program runs.

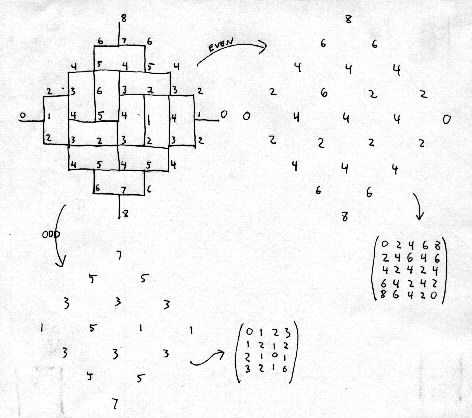
This example takes even diagonal groupings:
A=(0 2 4 6 8
   2 4 6 4 6
   4 2 4 2 4
   6 4 2 4 2
   8 6 4 2 0)
multiply it by one-half (A*.5):
A=(0 1 2 3 4
   1 2 3 2 3
   2 1 2 1 2
   3 2 1 2 1
   4 3 2 1 0)
convert to ASM ('-' means "-1") of size (n+1)x(n+1):
A=(0 0 1 0
   1 0 0 0
   0 1 - 1
   0 0 1 0)
Here's the ASM of the other (odd) diagonal grouping:
B=(0 1 0
   1 0 0
   0 0 1)
...which is a nxn permutation matrix.
Algorithm to convert matrices made from AD's into ASMs: Given submatrix
C=(a b
   c d)
ASM entry = { 0 if a+d=b+c , 1 if a+d=b+c-2 , -1 if a+d=b+c+2 }
Definition: ASMs are compatible if, when the small and large ASMs are converted to AD's, adjacent vertices differ by 1 or 3.
Question: For a given nxn ASM, how many compatible (n+1)x(n+1) ASMs are there?
Question: For a given (n+1)x(n+1) ASM, how many compatible nxn ASMs are there?
Number of positions free to change in smaller array is sum of "-1"'s in larger arrays ASMs.
Claim: An (n+1)x(n+1) ASM with k -1's is compatible with exactly 2^k nxn ASMs.
Claim: An nxn ASM with j +1's is compatible with exactly 2^j (n+1)x(n+1) ASMs.
Plot the locations of -1's in an ASM, and it might look like a circle, we think.
Bonus Questions:
(1) Show number of tilings of an order n AD that do not contain ``bad local conditions'' is equal to number of order n Baxter permutations.
(2) Prove the conjecture: the # of ASMs of order n that link up terminals as 1 to 2, 3 to 4, ..., (2n-1) to (2n) is exactly equal to the number of ASMs of order n-1.
Note: a -1 in the (n+1)x(n+1) represents something. ???

The Square Ice Model
0 + 0 0       0 1 2 3 4    
+ - 0 +   ==> 1 2 1 1 3 ==>  to the flux ==> rotated to get 
0 0 + 0       2 1 2 2 2      line vector     densly packed
0 0 0 0       3 2 3 3 1      field.          flux line field.
              4 3 2 2 0
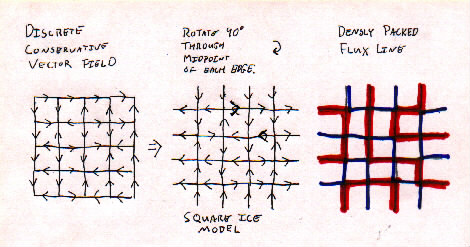
I need a good explanation of what is going on here! Can anyone help?
Matrix to Vector Field
each entry of the matrix coresponds to a node, and neighboring nodes have an edge in the direction of the one of which the coresponding entry in the matrix is bigger.
Vector Field to Square Ice
Take each edge and rotate it by -90degrees ('-' here means clockwise.) The center of each square from the vf is now a node in the si picture.
Square Ice to Densely Packed Flux
Take the nodes of the si and color them chessboard-wise. Now look at the shaded nodes. The edges that go AWAY from a shaded node we shall color blue and the arrows that go INTO a shaded node we shall deem red. And then omit the directions for the dpf picture.
When looking at the dense flux line graph of an ASM, with, say, 12 terminals, (numbered 1 - c) the number of ways to connect terminals 2 & 3 is equal to the number of ways to connect 3 & 4. This theorem was proved by Ben Wieland.
        1  2  3 
      c         
               4
      b	  
               5
      a         
               6
       9  8  7
Publishing:
There are three potential articles we have lined up:

Properties of tilings of different regions
Baxter permutations and domino tilings
Blue/green tilings