SSL Minutes
1 March 2001
Hal and Boytcho
People have things to say
Boytcho says that Mathematical Induction works for any well ordered set, such as the positive integers or the Cartesian product of a finite number of well ordered sets under the dictionary ordering. Someone forgets that the real numbers are not well ordered.
Hal asks what functionality should go into the program. He gets good feedback:
- Detect large chunks of same type of block (aka icebergs)
- Calculate Height Functions
- Add together two ADs (Eric Kuo's algorithm)
- Interactive and non-interactive modes.
- convert to ASM (in real time)
- Give lots of power to the interface.
Nick talks about how he's given some thought to representing a DPF (Dense Packed Flux). Example :
o---o---X---o
| | X |
XXXXXXXXX---o 4 6 8
| | | | ==> 1 5 4
o---XXXXXXXXX 2 9 1
| X | |
o---X---o---o
Each square is represented by a bitwise numbering system:
1
o---o
8 | | 2
o---o
4
Crash-course-type Intro to the Binary Number System: Traditionally humans use the symbols 0, 1, 2,... 9 to write numbers down. These are the ten digits. On those symbols is based the decimal (aka ``base ten'') number system. When we write down a number say 935, that means that the magnitude of it is obtained by the following formula 9*102 + 3*101 + 5*100 = 900 + 30 + 5. The position of each digit represents the power of ten that it is a coefficient for. We need exactly ten symbols for the base-ten representation of numbers to avoid a mess and have a unique representation for each number. Ten is a convenient number base for humans to work with, but not so for computers. They deal better with numbers represented in binary (base two). The symbols used are 0 and 1. (Traditionally to avoid ambiguity a subscript is used to indicate the base.) A binary number is 10012 for example. This is the number 1*23 + 0*22 + 0*21 + 1*20 = 910. The word digit is related to the decimal system in that it means one of the ten symbols used in it. Therefore with binary numbers we talk of bits (from Binary digIT). The numbers chosen by Nick above are all powers of two, which means that they have exactly one bit in their binary representation set to 1. Computers can easily be convinced to deal with numbers bit by bit. Another advantage of that choice is that the sum of the numbers corresponding to the ``on'' sides of a square never exceeds four bits, and its binary representation makes it immediately obvious which sides are ``on.''Add together the numbers of those sides that have flux lines on them. Then you get a nice matrix. You can flip a square if it is a 5 or a 10. Let's flip the 5 in the center of the matrix to a 10. This affects the four squares adjacent to it. Legal moves:
5 to a 10: 10 to a 5:
-4 +4
+2 +5 +8 -2 -5 -8
-1 +1
Then we get:
o---o---X---o
| | X |
4 2 8 XXXXX---X---o
flip--> 3 10 12 ==> | X X |
2 8 1 o---X---XXXXX
| X | |
o---X---o---o
Software
We get volunteers to look at redblue.c: Nick, Hal, Boytcho, Rachel. (http://jamespropp.org/hidden/ssl/blue-red.c)
We also need to find out what other software is out there: Abe, Nick.
Baxter Permutations I (Boytcho)
Let N be an odd element of the Natural Numbers. Let IN = {1, 2, 3, 4, ... N} Let ON be the odd elements of IN. Let EN be the even elements of IN.
Definition: P is a Baxter Permutation iff
- P(ON) = ON and P(EN) = EN
- if P(n) is between P(2i) and P(2i+1) then n >= 2i
- if P(n) is between P(2i) and P(2i-1) then n<= 2i
Baxter Permutations II (Mike)
The set of permutations on In is called Sn. If w is an element of Sn, w is Baxter iff for every i in {1, 2, 3, ... n-1}, it passes the test.
The Test. Let r = w-1(i). Let s = w-1(i+1). Assume r > k. If there exists a ki such that, for all t in [k,r], w(t) <= i and, for all u in [s,k], w(u) > i, then the test is passed.
Here's a case by case run down:
- If s < r Then we ask is there a k in [s, r] for which we know that P(s), ... P(k) are all <= i, and P(k+1),\dots P(r) are all > i?
- If r < s Then we ask is there a k in [r,s] for which we know that P(r), ... P(k) are all > i, and P(k+1), ... P(s) are all <= i?
- It is never the case that s = r.
Here is an example: we permute (1,2,3,4)--> (2,4,1,3). For i=1 we can partition in the following way 2,4,| 1. So we don't know yet this not to be a Baxter permutation. For i=2 we cannot however partition 2,4,1,3 in a way that would satisfy our question, thus we now know the permutation to not be a Baxter Permutation.
ASMs and Monotone Triangles
There is a nice correspondence between ASMs and Monotone Triangles.
0 1 0 0 0 0 1 0 0 0 2
1 - 1 0 0 1 0 1 0 0 1 3
0 0 0 1 0 <--> 1 0 1 1 0 <--> 1 3 4
0 1 0 0 0 1 1 1 1 0 1 2 3 4
0 0 0 0 1 1 1 1 1 1 1 2 3 4 5
ASM Intermediate Monotone Triangle
In each entry of the intermediuate matrix, add up the
entries of the ASM going down the column until you get
to the corresponding location. In other words,
the (i,j) (row, column) entry in the
intermediuate matrix is simply the sum from k = 1 to k = i of the
(k,j) entries in the ASM.
Note that the rows of the intermediate matrix add up to (1,2,3,4,5)T.
Now, we ask the question: ``For each row of the intermediate matrix, which columns hold 1's?'' The answer to that is the monotone triangle.
Properties of the monotone triangle (MT).
B
A <= B / \ B <= C
/ \
A-----C
A < C
Usefulness: It is easy to generate MTs. (bluered.c)
Plane Partitions and Semi-Strict Gelfand Patterns
What is a partition of a number? A set of positive numbers that add up to it. 10 = 6+4 or 10 = 5+3+2.
Partition Ferrer's Diagram
5 .....
3 --> ...
2 ..
A Plane Partition has a three dimentional graph, not a 2 dimentional graph. Here's an example Partition:
3 2 1 1 2 3 7 8 9
2 1 --> Boxes in three Space. --> 1 2 4 7 8
1 2 5 7
1 3 6
1 4
1
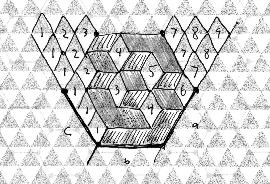
Stack them as boxes inside a cube. Then think of that cube as equivilent to a hexagon tiles with lozenges. Draw that. Then extend the cornes out, as shown in the graph. Number the vertically oriented lozenges based on the distance from the line on the left side. Transfer the numbers into a triangle. That's a Semi-Strict Gelfand Pattern.
Properties of the Semi-Strict Gelfand Pattern:
A < C
A-----C
\ /
A <= B \ / B < C
B
Why was that important?