SSL Minutes
27 March 2001
Dominic and Hal
Etcetera
Jim has assumes responsibility for spending the interest off of a $5000 endowment that a former undergrad has given the department to be spent on games. Any ideas? By the way, 5% of $5000 is $250.
Joel will bring the beverage for Thursday.
Undergraduate Research Symposium
The Undergraduate Research Symposium (URS) is quickly approaching. We need to decide what we will all have at the URS. We generated a rough list of topics, people responsible for different topics, and materials we need:
Topics
- TOAD BACKGROUND
- what is it? (Hal)
- shuffling (Hal)
- lozenges (Rachel)
- ALTERNATING SIGN MATRICES
- definition (Geir)
- relation to TOADs (Kristin)
- as DPFLs (Geir)
- CONJECTURES
- Baxter Permutations (Dominic and Nick)
- ASM shuffling conjecture (Boytcho)
- A(n-1) conjecture (also known as the proper linking conjecture)
- INTERESTS
- lozenge tiling flux lines (Rachel)
- probability of certain ASMs (Pavle)
- DPFL linking probabilities (Kristin)
Materials
- COMPUTER
- Jim will bring his laptop
- Hal will send a tarball with programs
- T-SHIRTS
When preparing a paragraph, picture, or presentation of the assigned topics, people should scan in necessary images, send the images to Boytcho, and send images and text to Rachel who will compile everything. Boytcho will make all of the images look nice with xfig.
Volunteers to attend the URS, and the times they are available:
- Hal: 9:00-10:00, 12:30-end.
- Kristin: 12:00-2:00
- Joel: 9:00-1:00
- Dan: 2:30-5:00
- Nick: 2:30-5:00
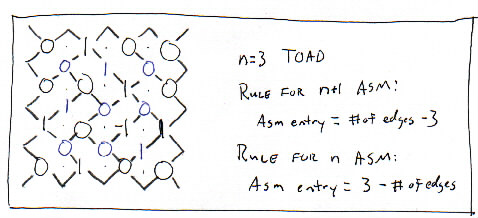
To show the relationship between Aztec Diamonds and ASMs at the URS, we do not have to explain height function or the algorithm used to find the ASMs from these heights. Instead, we can use a simpler method:
Look at the vertices in an Aztec Diamond that correspond to the entries of the larger (size n+1) ASM. Count the number of edges that meet at each vertex. This number will be a 2, 3, or 4. Subtract 3 from the number (this will yield a -1, 0, or 1). This produces an ASM from any tiling of an Aztec Diamond.
We can use a similar method to find the smaller (size n) ASM. Count the number of edges that meet at each vertex. This number will be a 2, 3, or 4. Subtract this number from 3 (this will yield a -1, 0, or 1). This produces an ASM from any tiling of an Aztec Diamond.
Mathematics
A Question (perhaps for Pavle): can we prove or even verify this conjecture?
Conjecture: If x and y are two different n-by-n ASMs, then the number of size n+1 ASMs that are compatible with both x and y is equal to the number of size n-1 ASMs that are compatible with both x and y.
In other words, if x and y are two different nodes on the same level of the ASM tree diagram, is the number of way to connect them by going up one level and back down is equal to the number of way to connect them by going down one level and back up.
Question: (posed by Joel and Geir) How many ASMs are there with only one -1? with two -1s? More?
Partial Answer: If there are A(n) ASMs of size n, there are A(n) - n! ASMs with one or more -1's in them. There are (n choose 3)2*(n-3)! ASMs with one -1.
Question: How many ways are there to go up k levels, starting from the bottom? (1,2,8,80,...) Maybe there's a nice theorem lurking there.
Jim's article titled "The Many Faces of Alternating Sign Matrices" is due by April 20th. So everybody should prove important stuff by then.
Rachel asks: What does p-adic continuity mean?
That leads to a Conjecture: The number of domino tilings of an n-by-2n rectangle is always odd. (Can we prove this by showing that for any n, we can match Dominos into pairs with a remaining singleton?)
Abe asks about Components and Linkages. He wants to know a good way to count the number of components of a matching. Jim gives a good answer: First, see what even number 1 matches with. Next, move one place to the right. See what even number this number matches with. Again, move one place to the right. See what even number this number matches with. etc.
Baxter Permutations
Dominic: What's the deal with the two different definitions of Baxter Permutations? For example, one definition works only on odd numbers. Another definition works on any number. How do these two definitions relate?
Note: Hal will introduce some notation into the notes. I hope this helps.
The object of interest here is an order n Aztec Diamond where both of the corresponding ASMs are permutation matrices. (An ASM without -1's is a permutation.)
If we take a size n+1 permutation matrix, there is exactly one size n compatible ASM, because we know that the number of of smaller compatible ASMs are 2^(# of -1s in the bigger ASM) = 2^0 = 1. This smaller ASM may or may not be a permutation matrix. If it is a permutation, then we conjecture that the size n+1 ASM is a type II Baxter permutation.
What is the difference between a Type I Baxter Permutation and a Type II Baxter Permutation? A type I permutation is odd in size (2n+1), and sends odds to odds and evens to evens. If we take out the odd elements of the type I Baxter Permutation (1BP) we get a size n+1 Type II Baxter Permutation (2BP). We think that each 2BP corresponds with exactly one size n permutation that, when put together, form a 1BP.
According to the Baxter Permutation Conjecture, each size n+1 2BP is identical to a size n+1 ASM without -1's whose single compatible size n ASM is also has no -1's. Furthermore, if we construct a permutation matrix Pi,j of size 2n+1 where if i and j are odd, they correspond to entries of the size n+1 ASM and if i and j are both even, they correspond to entries of the size n ASM, and if i and j are not both odd or even, the entry is zero; then P is a 1BP corresponding to the original 2BP.
Example 1
+ 0 0 0 + 0 0
0 + 0 and + 0 0 0 are compatible.
0 0 + 0 0 + 0
0 0 0 +
As permutations:
2 4 6 and 3 1 5 7
We can rewrite that by interspersing the ASMs:
0 + 0 0 0 0 + 0 0 0 0 + 0 0 0 + 0 0 0 0 0 + 0 0 0 + 0 0 0 0 0 0 0 + 0 --> 0 0 0 + 0 0 0 --> 3 2 1 4 5 6 7 0 0 + 0 0 0 0 0 + 0 0 0 0 + 0 0 0 0 0 + 0 0 0 0 + 0 0 0 0 0 0 +For example: 3 1 5 7 (1 maps to 3, 3 maps to 1, 5 and 7 map to themselves) induces 2 4 6 (each maps to itself). Thus we have 3157 and 246. But we can write these two permutations as one larger permutation as follows: 3214567.
Question: How does a size n+1 2BP ``induce'' a size n permutation?
Example 2
0 0 + 0 0 0 +
0 + 0 and 0 0 + 0 are compatible.
+ 0 0 + 0 0 0
0 + 0 0
As permutations, we can write them as 3 2 1 and 3 4 2 1.
We claim that 3 4 2 1 is a 2BP.
We can construct a 1BP from these two permutations: 3 2 1, 3 4 2 1 --> 6 4 2, 5 7 3 1 --> 5 6 7 4 3 2 1
Conclusion: We seem to have missed the big clue that was set out in front of us: the existence of two types of Baxter Permutations, along with the fact that a TOAD corresponds to two ASMs.