SSL Minutes
26 April 2001
Hal
Jim Asks what Pavle passed on to people. Should we check the notes?
Jim asked about the up-down conjecture. We told him that the next big programming push will be to check that out.
Kristin should email out her results (linking probability numbers) soon (DONE).
Question: What are the average number of components of the DPFL/FLP/EIEIO matchings? Abe will look at that.
That led to another question: What is the proper way of counting components? There are two natural answers:
- Break the DPFL/FLP between 2n and 1.
- Take the max number of components that can be produced by breaking the DPFL/FLP at any place.
We heard a story about where the gyrational symmetry came from. The theorem was first stated as something that was obviously not true all the time, but then it turned out that it was. The moral of our story has something to do with our intuition.
I forced Rachel to take a stand on whether she believes in gyrational symmetry for Hexagons. She says no, but was unwilling to place money on it.
Rachel then talked about her theorem about the lack of what would be a distal matching of an ASM-DPFL in hex-DPFLs. The thing that Jim called a hole in her proof has been proved, but Rachel did not explain how she filled it very well. But I understood.
We talked about the stupid t-shirts.
The Last Supper will be on the 17th at 6pm. We will not be eating at Domino's Pizza. Somebody noted that we have the right number of people for the last supper (12+1).
The VIGRE Lunch
Wednesday the 2nd at 12:00pm.
I am still confused about this. Do I have to prepare anything for this?
The whole week after this (6-12th), Jim will be in the Black Forrest.
Back to the lunch: Topics will include the Baxter theorem and HexDpfl's. Jim will talk, then he'll open things up for general discussion.
I ask about local moves. Jim says a good way to check would be with the 7 proximal DPFLs of a given size.
Abe can get to work on programming now that he's finished the paper he had to write.
Nick wants a web account. I got out my magic wand and gave him one.
Dominic wants to work on the big size 2n+1 ASM that comes from smushing two compatible ASMs together.
Rachel asks a question. It turns out she was asking about fault free rectangle tilings.
The Razamov-Stroganov Game
Here is the game: First, pick an N. Then pick a size N square DPFL: we'll call this one the target. There are two players.
- Player A randomly chooses a DPFL. He wins if his DPFL has the same matching as the target.
- Player B randomly chooses a DPFL. She then makes exactly one random mutation to the matching from her DPFL. If the resulting matching is identical to the target's matching, she wins.
Definition of Mutation: pick two adjacent terminals i and (i+1)mod(2n). suppose i connects to j and (i+1)mod(2n) connects to k. Reconnect i to (i+1)mod(2n), and j to k. It is possible that i might equal k to begin with, in which case this mutation changes nothing.
Conjecture: Players A and B have the SAME chance of winning!
Proof for N=3.
There are 5 matchings for this size: two are proximal (P1 and P2), and three are distal (D1, D2, and D3)
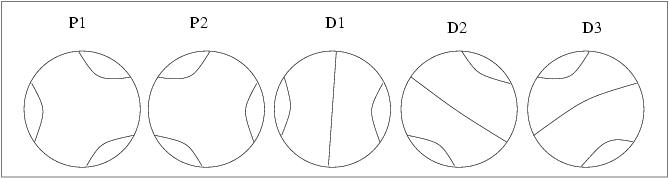
Table of probabilities:
P(A) P1 P2 D1 D2 D2 P(B)
-----------------------
2/7 P1 | 3/6 0/6 1/6 1/6 1/6 | 2/7
2/7 P2 | 0/6 3/6 1/6 1/6 1/6 | 2/7
1/7 D1 | 2/6 2/6 2/6 0/6 0/6 | 1/7
1/7 D2 | 2/6 2/6 0/6 2/6 0/6 | 1/7
1/7 D3 | 2/6 2/6 0/6 0/6 2/6 | 1/7
Look at this as a matrix equation:
2/7 3/6 0/6 1/6 1/6 1/6 2/7
2/7 0/6 3/6 1/6 1/6 1/6 2/7
1/7 = 2/6 2/6 2/6 0/6 0/6 * 1/7
1/7 2/6 2/6 0/6 2/6 0/6 1/7
1/7 2/6 2/6 0/6 0/6 2/6 1/7
This relates to the all-pervasive eigenvalue problem.
Homework: Do this for n=4.
From propp@math.wisc.edu Tue May 1 13:45:00 2001
Date: Tue, 1 May 2001 13:28:38 -0500 (CDT)
From: propp@math.wisc.edu
To: hwcanary@students.wisc.edu
Subject: homework assignmentI think you asked for this:
Read Razumov and Stroganov's new article! And then see if you believe my new
Conjecture: the relations given by their Conjecture 1, in combination with the fact that each distal linking-pattern arises from exactly 1 ASM, and in combination with the symmetry property proved by Wieland, suffice to determine the number of ASMs that give rise to each linking pattern, and in particular, the total number of ASMs.
Proof for n=3. There are only two geometries that a linking-pattern can have in this case: proximal and distal. Let P (resp. D) be the number of ASMs corresponding to any given proximal (resp. distal) linking-pattern. Pretend for the moment that we don't know P and D. Since there are 2 proximal and 3 distal linking-patterns, the total number of ASMs is N = 2P+3D. If the fixed link-pattern that the players are aiming for is the distal pattern 1<-->6, 2<-->5, 3<-->4, then player A has a chance of winning equal to
(*) D/NNow let's compute player B's chances. For each of the five linking patterns that he could have started with, I give the probability that he could end up with 1<-->6, 3<-->4, 5<-->2:
1<-->2, 3<-->4, 5<-->6 (proximal): 1/6 1<-->2, 3<-->6, 5<-->4 (distal): 0/6 1<-->4, 3<-->2, 5<-->6 (distal): 0/6 1<-->6, 3<-->2, 5<-->4 (proximal): 1/6 1<-->6, 3<-->4, 5<-->2 (distal): 2/6So B's chance of winning is
(P/N)(1/6)+(D/N)(0/6)+(D/N)(0/6)+(P/N)(1/6)+(D/N)(2/6)or
(**) (P/3+D/3)/NComparing (**) with (*), we see that the RS conjecture implies
P/3 + D/3 = Dwhich reduces to
P = 2D.But now we pull out the fact that each distal linking-pattern arises from exactly 1 ASM. This gives us D=1, and the formula P = 2D now gives us P = 2, so we've calculated everything we want to know, and the number of ASMs of order 3 is N = 2P+3D = (2)(2)+(3)(1) = 7.
Homework (everybody!): For Tuesday, determine whether my conjecture is true for n=4.
Keep in mind that Ben Wieland has a different conjecture, which relates A_n(pi) to A_{n+1}(pi') where pi is a linking-pattern of order n and pi' is a linking pattern of order n+1. Even if the Razumov-Stroganov relations don't suffice to force the values of all the A_n(pi)'s, maybe they do when taken together with the Wieland relations (or other relations that you guys are about to discover!).
And if we can find enough relations to force the values of all the A_n(pi)'s, then we're halfway towards discovering (among other lovely things) a new proof of the original ASM conjecture, totally different from both Doron Zeilberger's proof and Greg Kuperberg's proof!
Jim
We retired to B107, and I made a pretty hexDpfl picture for the stupid t-shirt. Don't know what others did. Then Rachel, Boytcho, and I went and had ice cream and beer.