Matchmaker.com: Sign up now for a free trial. Date Smarter!

1. Introduction
2. Huffman Coding
3. Lempel-Ziv Coding
4. Notes
5. References

I. Introduction
  The main objective of this page is to introduce two important lossless compression algorithms: Huffman Coding and Lempel-Ziv Coding. A Huffman encoder takes a block of input characters with fixed length and produces a block of output bits of variable length. It is a fixed-to-variable length code. Lempel-Ziv, on the other hand, is a variable-to-fixed length code. The design of the Huffman code is optimal (for a fixed blocklength) assuming that the source statistics are known a priori. The Lempel-Ziv code is not designed for any particular source but for a large class of sources. Surprisingly, for any fixed stationary and ergodic source, the Lempel-Ziv algorithm performs just as well as if it was designed for that source. Mainly for this reason, the Lempel-Ziv code is the most widely used technique for lossless file compression.
 

II. Huffman Coding
  The basic idea in Huffman coding is to assign short codewords to those input blocks with high probabilities and long codewords to those with low probabilities. This concept is similar to that of the Morse code.

A Huffman code is designed by merging together the two least probable characters, and repeating this process until there is only one character remaining. A code tree is thus generated and the Huffman code is obtained from the labeling of the code tree. An example of how this is done is shown below.

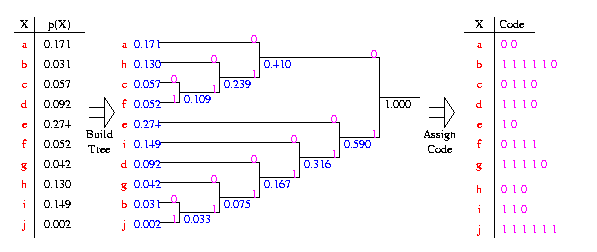
• It does not matter how the characters are arranged. I have arranged it above so that the final code tree looks nice and neat.
• It does not matter how the final code tree are labeled (with 0s and 1s). I chose to label the upper branches with 0s and the lower branches with 1s.
• There may be cases where there is a tie for the two least probable characters. In such cases, any tie-breaking procedure is acceptable.
• Huffman codes are not unique.
• Huffman codes are optimal in the sense that no other lossless fixed-to-variable length code has a lower average rate.
• The rate of the above code is 2.94 bits/character.
• The entropy lower bound is 2.88 bits/character.

III. Lempel-Ziv Coding
  The Lempel-Ziv algorithm is a variable-to-fixed length code. Basically, there are two versions of the algorithm presented in the literature: the theoretical version and the practical version. Theoretically, both versions perform essentially the same. However, the proof of the asymptotic optimality of the theoretical version is easier. In practice, the practical version is easier to implement and is slightly more efficient. We explain the practical version of the algorithm as explained in the book by Gersho and Gray and in the paper by Welch.

The basic idea is to parse the input sequence into non-overlapping blocks of different lengths while constructing a dictionary of blocks seen thus far.
 
  Encoding Algorithm

1. Initialize the dictionary to contain all blocks of length one (D={a,b}).
2. Search for the longest block W which has appeared in the dictionary.
3. Encode W by its index in the dictionary.
4. Add W followed by the first symbol of the next block to the dictionary.
5. Go to Step 2.

Click here to see the animation
(it takes about 2 minutes to loop through the animation)

• Theoretically, the size of the dictionary can grow infinitely large.
• In practice, the dictionary size is limited. Once the limit is reached, no more entries are added. Welch had recommended a dictionary of size 4096. This corresponds to 12 bits per index.
• The length of the index may vary. For example, in the n-th block, the current dictionary size is n+1 (assuming that the limit has not been reached). Therefore, we can encode the index of block n using [log₂(n+1)] bits (rounded up to the nearest integer). For example, the first index can be represented by 1 bit, the 2nd and 3rd by 2 bits each, the 4th, 5th, 6th, and 7th by 3 bits each, and so on. This is the variable-to-variable length version of the Lempel-Ziv algorithm.
• For a maximum dictionary size of 2^m, variable-length encoding of the indices saves exactly 2^m-1 bits compared to fixed-length encoding.
• The above example, as most other illustrative examples in the literature, does not result in real compression. Actually, more bits are used to represent the indices than the original data. This is because the length of the input data in the example is too short.
• In practice, the Lempel-Ziv algorithm works well (lead to actual compression) only when the input data is sufficiently large and there are sufficient redundancy in the data.
• Decompression works in the reverse fashion. The decoder knows that the last symbol of the most recent dictionary entry is the first symbol of the next parse block. This knowledge is used to resolve possible conflict in the decoder.
• Many popular programs (e.g. Unix compress and uncompress, gzip and gunzip, and Windows WinZip) are based on the Lempel-Ziv algorithm.
• The name ``Ziv-Lempel'' is more appropriate than ``Lempel-Ziv'' (see Gersho and Gray and the name ordering in References 3 and 4 below).

IV. Notes

• The following table compares an adaptive version of the Huffman code (implemented in the Unix ``compact'' program) and an implementation of the Lempel-Ziv algorithm (Unix ``compress'' program).

  	Adaptive Huffman	Lempel-Ziv
  LaTeX file	66%	44%
  Speech file	65%	64%
  Image file	94%	88%
  Size of compressed file as percentage of the original file

  
   
• The large text file described in the Statistical Distributions of English Text (containing the seven classic books with a 27-letter English alphabet) has a compression ratio of 36.3% (original size=5086936 bytes, compressed size=1846919, using the Linux ``gzip'' program). This corresponds to a rate of 2.9 bits/character --- compared with the entropy rate of 2.3 bits/character predicted by Shannon. This loss of optimality is most likely due to the finite dictionary size.

V. References

1. A. Gersho and R. M. Gray, Vector Quantization and Signal Compression.
2. D. A. Huffman, ``A Method for the Construction of Minimum Redundancy Codes,'' Proceedings of the IRE, Vol. 40, pp. 1098--1101, 1952.
3. J. Ziv and A. Lempel, ``A Universal Algorithm for Sequential Data Compression,'' IEEE Transactions on Information Theory, Vol. 23, pp. 337--342, 1977.
4. J. Ziv and A. Lempel, ``Compression of Individual Sequences Via Variable-Rate Coding,'' IEEE Transactions on Information Theory, Vol. 24, pp. 530--536, 1978.
5. T. A. Welch, ``A Technique for High-Performance Data Compression,'' Computer, pp. 8--18, 1984.

Nam Phamdo
Department of Electrical and Computer Engineering
State University of New York
Stony Brook, NY 11794-2350
phamdo@ieee.org