|
Info on Grad
Schools:
Buy Books, CDs, &
Videos:
Digital Camera:
Rio MP3 Player:
Diamond
Rio 500 Portable MP3 Player
Memory Upgrade:
$1.23 per issue:
Ebay Auction:
$1.83 per issue:
Info on Grad
Schools:
Buy Books, CDs, &
Videos:
Digital Camera:
Rio MP3 Player:
Diamond
Rio 500 Portable MP3 Player
Memory Upgrade:
$1.23 per issue:
Ebay Auction:
$1.83 per issue:
Info on Grad
Schools:
Buy Books, CDs, &
Videos:
Digital Camera:
Rio MP3 Player:
Diamond
Rio 500 Portable MP3 Player
Memory Upgrade:
$1.23 per issue:
Ebay Auction:
$1.83 per issue:
Info on Grad
Schools:
Buy Books, CDs, &
Videos:
Digital Camera:
Rio MP3 Player:
Diamond
Rio 500 Portable MP3 Player
Memory Upgrade:
$1.23 per issue:
Ebay Auction:
$1.83 per issue:
Info on Grad
Schools:
Buy Books, CDs, &
Videos:
Digital Camera:
Rio MP3 Player:
Diamond
Rio 500 Portable MP3 Player
Memory Upgrade:
$1.23 per issue:
Ebay Auction:
$1.83 per issue: |
![]()

Find Online Degrees
Speech Compression
Contents
- Introduction
- LPC
Modeling
- LPC
Analysis
- 2.4
kbps LPC Vocoder
- 4.8
kbps CELP Coder
- 8.0
kbps CS-ACELP Coder
- Demonstration
- References
I. Introduction
The compression of speech signals has many practical
applications. One example is in digital cellular technology where many
users share the same frequency bandwidth. Compression allows more users to
share the system than otherwise possible. Another example is in digital
voice storage (e.g. answering machines). For a given memory size,
compression allows longer messages to be stored than otherwise.
Historically, digital speech signals are sampled at a rate of 8000
samples/sec. Typically, each sample is represented by 8 bits (using
mu-law). This corresponds to an uncompressed rate of 64 kbps (kbits/sec).
With current compression techniques (all of which are lossy), it is
possible to reduce the rate to 8 kbps with almost no perceptible loss in
quality. Further compression is possible at a cost of lower quality. All
of the current low-rate speech coders are based on the principle of
linear predictive coding (LPC) which is presented in the following
sections.
II. LPC Modeling
A.
Physical Model:
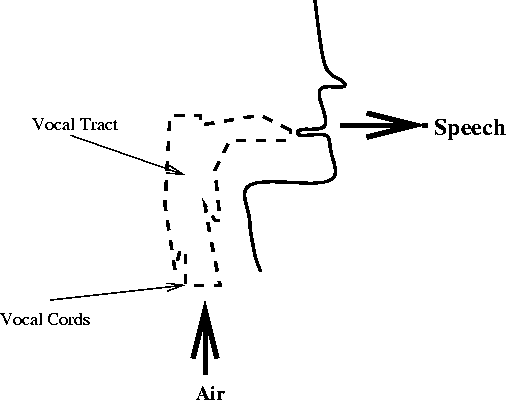
When you speak:
- Air is pushed from your lung through your vocal tract and out of
your mouth comes speech.
- For certain voiced sound, your vocal cords vibrate (open and
close). The rate at which the vocal cords vibrate determines the
pitch of your voice. Women and young children tend to have high
pitch (fast vibration) while adult males tend to have low pitch (slow
vibration).
- For certain fricatives and plosive (or unvoiced) sound, your
vocal cords do not vibrate but remain constantly opened.
- The shape of your vocal tract determines the sound that you make.
- As you speak, your vocal tract changes its shape producing different
sound.
- The shape of the vocal tract changes relatively slowly (on the scale
of 10 msec to 100 msec).
- The amount of air coming from your lung determines the loudness of
your voice.
B. Mathematical Model:

- The above model is often called the LPC Model.
- The model says that the digital speech signal is the output of a
digital filter (called the LPC filter) whose input is either a train of
impulses or a white noise sequence.
- The relationship between the physical and the mathematical
models:
| Vocal Tract |
 |
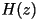 (LPC Filter)
(LPC Filter) |
| Air |
 |
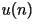 (Innovations)
(Innovations) |
| Vocal Cord Vibration |
 |
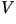 (voiced)
(voiced) |
| Vocal Cord Vibration Period |
 |
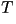 (pitch period)
(pitch period) |
| Fricatives and Plosives |
 |
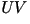 (unvoiced)
(unvoiced) |
| Air Volume |
 |
 (gain)
(gain) |
- The LPC filter is given by:
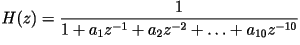 which is equivalent to saying that the
input-output relationship of the filter is given by the linear
difference equation: which is equivalent to saying that the
input-output relationship of the filter is given by the linear
difference equation:
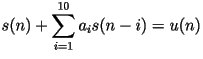
- The LPC model can be represented in vector form as:

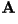 changes every 20 msec or so. At a sampling rate of 8000
samples/sec, 20 msec is equivalent to 160 samples. changes every 20 msec or so. At a sampling rate of 8000
samples/sec, 20 msec is equivalent to 160 samples.
- The digital speech signal is divided into frames of size 20
msec. There are 50 frames/second.
- The model says that
 is equivalent to is equivalent to
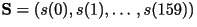 Thus the 160 values of Thus the 160 values of 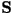 is
compactly represented by the 13 values of is
compactly represented by the 13 values of 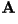 . .
- There's almost no perceptual difference in
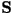 if: if:
- For Voiced Sounds (V): the impulse train is shifted
(insensitive to phase change).
- For Unvoiced Sounds (UV):} a different white noise sequence
is used.
- LPC Synthesis: Given
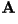 ,
generate ,
generate 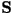 (this is done using standard filtering
techniques). (this is done using standard filtering
techniques).
- LPC Analysis: Given
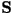 , find
the best , find
the best 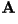 (this is described in the next section). (this is described in the next section).
III. LPC Analysis
- Consider one frame of speech signal:
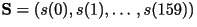
- The signal
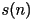 is related to the innovation is related to the innovation 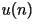 through
the linear difference equation: through
the linear difference equation:
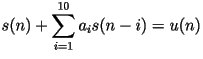
- The ten LPC parameters
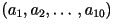 are
chosen to minimize the energy of the innovation: are
chosen to minimize the energy of the innovation:
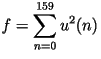
- Using standard calculus, we take the derivative of
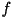 with
respect to with
respect to  and set it to zero: and set it to zero:
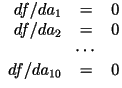
- We now have 10 linear equations with 10 unknowns:
 where where

- The above matrix equation could be solved using:
- The Gaussian elimination method.
- Any matrix inversion method (MATLAB).
- The Levinson-Durbin recursion (described below).
- Levinson-Durbin Recursion:
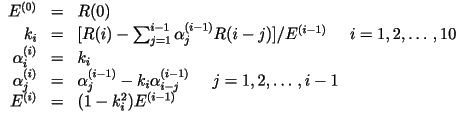 Solve the above for Solve the above for 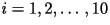 , and
then set , and
then set
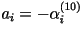
- To get the other three parameters:
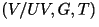 , we
solve for the innovation: , we
solve for the innovation:
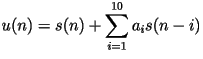
- Then calculate the autocorrelation of
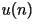 : :
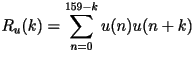
- Then make a decision based on the autocorrelation:
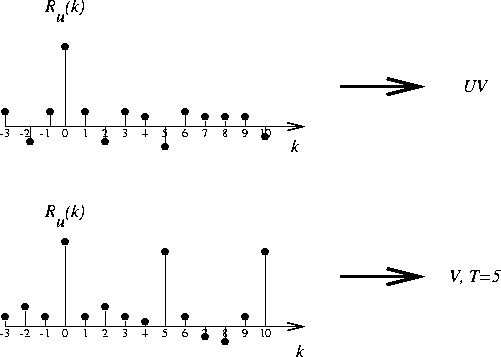
IV. 2.4kbps LPC Vocoder
- The following is a block diagram of a 2.4 kbps LPC Vocoder:
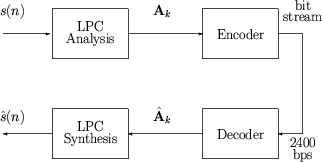
- The LPC coefficients are represented as line spectrum pair
(LSP) parameters.
- LSP are mathematically equivalent (one-to-one) to LPC.
- LSP are more amenable to quantization.
- LSP are calculated as follows:
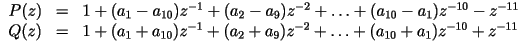
- Factoring the above equations, we get:
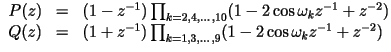 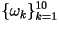 are
called the LSP parameters. are
called the LSP parameters.
- LSP are ordered and bounded:
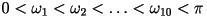
- LSP are more correlated from one frame to the next than LPC.
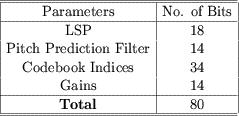
- The frame size is 20 msec. There are 50 frames/sec. 2400 bps is
equivalent to 48 bits/frame. These bits are allocated as follows:

- The 34 bits for the LSP are allocated as follows:

- The gain,
 , is encoded using a 7-bit non-uniform scalar
quantizer (a 1-dimensional vector quantizer). , is encoded using a 7-bit non-uniform scalar
quantizer (a 1-dimensional vector quantizer).
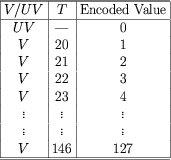
- For voiced speech, values of
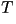 ranges
from 20 to 146. ranges
from 20 to 146.  are jointly encoded as follows: are jointly encoded as follows:
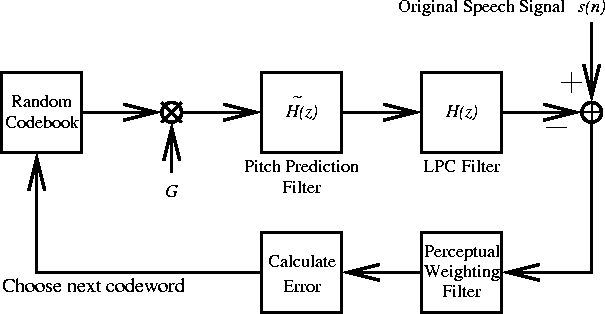
V. 4.8 kbps CELP Coder
- CELP=Code-Excited Linear Prediction.
- The principle is similar to the LPC Vocoder except:
- Frame size is 30 msec (240 samples)
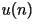 is coded directly is coded directly
- More bits are need
- Computationally more complex
- A pitch prediction filter is included
- Vector
quantization concept is used
- A block diagram of the CELP encoder is shown below:
- The pitch prediction filter is given by:
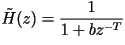 where where 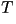 could
be an integer or a fraction thereof. could
be an integer or a fraction thereof.
- The perceptual weighting filter is given by:
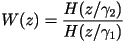 where where 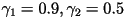 have
been determined to be good choices. have
been determined to be good choices.
- Each frame is divided into 4 subframes. In each subframe, the
codebook contains 512 codevectors.
- The gain is quantized using 5 bits per subframe.
- The LSP parameters are quantized using 34 bits similar to the LPC
Vocoder.
- At 30 msec per frame, 4.8 kbps is equivalent to 144 bits/frame.
These 144 bits are allocated as follows:
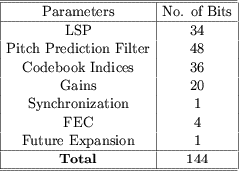
VI. 8.0 kbps CS-ACELP
- CS-ACELP=Conjugate-Structured Algebraic CELP.
- The principle is similar to the 4.8 kbps CELP Coder except:
- Frame size is 10 msec (80 samples)
- There are only two subframes, each of which is 5 msec (40 samples)
- The LSP parameters are encoded using two-stage vector
quantization.
- The gains are also encoded using vector
quantization.
- At 10 msec per frame, 8 kbps is equivalent to 80 bits/frame. These
80 bits are allocated as follows:
VII. Demonstration
This is a demonstration of five different speech compression
algorithms (ADPCM, LD-CELP, CS-ACELP, CELP, and LPC10).
To use this
demo, you need a Sun Audio (.au) Player. To distinguish subtle differences
in the speech files, high-quality speakers and/or headphones are
recommended. Also, it is recommended that you run this demo in a quiet
room (with a low level of background noise).
"A lathe is a big tool. Grab every dish of
sugar."
 Original
(64000 bps) This is the original speech signal sampled at 8000
samples/second and u-law quantized at 8 bits/sample. Approximately 4
seconds of speech. Original
(64000 bps) This is the original speech signal sampled at 8000
samples/second and u-law quantized at 8 bits/sample. Approximately 4
seconds of speech.
 ADPCM
(32000 bps) This is speech compressed using the Adaptive
Differential Pulse Coded Modulation (ADPCM) scheme. The bit rate is 4
bits/sample (compression ratio of 2:1). ADPCM
(32000 bps) This is speech compressed using the Adaptive
Differential Pulse Coded Modulation (ADPCM) scheme. The bit rate is 4
bits/sample (compression ratio of 2:1).
 LD-CELP
(16000 bps) This is speech compressed using the Low-Delay Code
Excited Linear Prediction (LD-CELP) scheme. The bit rate is 2
bits/sample (compression ratio of 4:1). LD-CELP
(16000 bps) This is speech compressed using the Low-Delay Code
Excited Linear Prediction (LD-CELP) scheme. The bit rate is 2
bits/sample (compression ratio of 4:1).
 CS-ACELP
(8000 bps) This is speech compressed using the Conjugate-Structured
Algebraic Code Excited Linear Prediction (CS-ACELP) scheme. The bit rate
is 1 bit/sample (compression ratio of 8:1). CS-ACELP
(8000 bps) This is speech compressed using the Conjugate-Structured
Algebraic Code Excited Linear Prediction (CS-ACELP) scheme. The bit rate
is 1 bit/sample (compression ratio of 8:1).
 CELP
(4800 bps) This is speech compressed using the Code Excited Linear
Prediction (CELP) scheme. The bit rate is 0.6 bits/sample (compression
ratio of 13.3:1). CELP
(4800 bps) This is speech compressed using the Code Excited Linear
Prediction (CELP) scheme. The bit rate is 0.6 bits/sample (compression
ratio of 13.3:1).
 LPC10
(2400 bps) This is speech compressed using the Linear Predictive
Coding (LPC10) scheme. The bit rate is 0.3 bits/sample (compression
ratio of 26.6:1). LPC10
(2400 bps) This is speech compressed using the Linear Predictive
Coding (LPC10) scheme. The bit rate is 0.3 bits/sample (compression
ratio of 26.6:1).
VIII. References
- L. R. Rabiner and R. W. Schafer, Digital
Processing of Speech Signals.
- N. Morgan and B. Gold, Speech
and Audio Signal Processing : Processing and Perception of Speech and
Music.
- J. R. Deller, J. G. Proakis, and J. H. L. Hansen, Discrete-Time
Processing of Speech Signals.
- S. Furui, Digital
Speech Processing, Synthesis and Recognition.
- D. O'Shaughnessy, Speech
Communications : Human and Machine.
- A. J. Rubio Ayuso and J. M. Lopez Soler, Speech
Recognition and Coding : New Advances and Trends.
- M. R. Schroeder, Computer
Speech: Recognition, Compression, Synthesis.
- B. S. Atal, V. Cuperman, and A. Gersho, Speech
and Audio Coding for Wireless and Network Applications.
- B. S. Atal, V. Cuperman, and A. Gersho, Advances
in Speech Coding.
- D. G. Childers, Speech
Processing and Synthesis Toolboxes.
- R. Goldberg and L. Rick, A
Practical Handbook of Speech Coders.
Nam Phamdo
Department of Electrical and Computer Engineering
State University of New York
Stony Brook, NY 11794-2350
phamdo@ieee.org
|







































