Spatial Systems Lab
Minutes
Contents
SSL Minutes
1 Feb 2001
Hal and Geir
Jim Propp Talks about SSL.
Each individual is expected to create something (code,
illustrations, documents, proofs).
Slogan: ``Teach what you know, learn what you don't, document
everything.''
Grant Proposal.
Somebody is in charge of keeping the Glossary.
Disseminate everything on the web.
Shared Bonuses. For example, Prove the Baxter Permutation
Conjecture for an hour's extra pay (for everybody).
Earn an extra hour's wages by attending Combinatorics Seminar
2:25-3:15 M 903 VV (next week only)
Get Time Cards. 2nd floor VV. Hand it to Propp or put it in his
mailbox. Today counts as work.
We can spend money on supplies, for example, books. We have a
LaTeX book somewhere.
Homework #1: Count the number of Domino tilings for 2xN
rectangle, for n<=10. There is a pattern there. Find it and
exploit it.
Public Web Site:
http://jamespropp.org/SSL/
There is a private web site and an email list.
Accounts on dodgeson will be done on Thursday.
Mathematics:
We know some things about an Aztec Diamond. But what about a
rectangle or square?
The number of domino tilings of a 2n-by-2n square is:
\begin{displaymath}
\product_{j=1}^n \product_{k=1}^n
(4 \cos^2 \frac{\pi j}{2n+1}
+ 4 \cos^2 \frac{\pi k}{2n+1})
\end{displaymath}
Is it an integer? Yes: you can use Galois theory to show that it's
a rational number and algebraic number theory to show that it's an
"algebraic integer". The only numbers that are both rational and
algebraic integers are integers.
To prove that something is an integer:
(1) Cook up a combinatorial problem it describes
(2) Reverse engineer the algebra.
A different kind of tiling problem.
Domino vs. Lozenge tilings: (Fig 1 and 2)
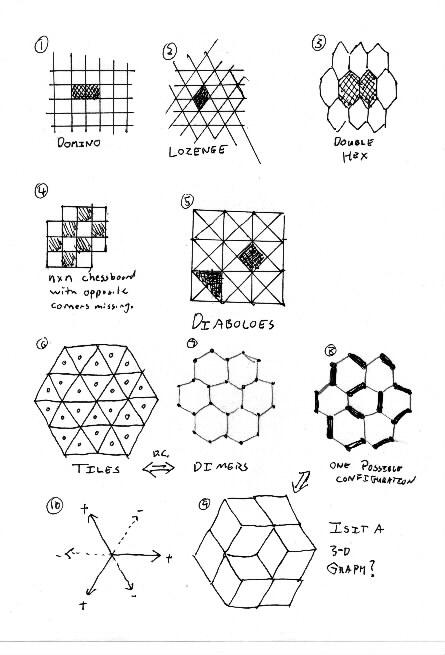
Dominos are 1x2 rectangles in a grid. Lozenges are two touching
equilateral triangles.
Double-Hexes (Fig 3) don't do anything cool, because they don't
have height functions.
Not all areas are tilable: Hal asks about the nxn chessboard
missing two opposite corners. (Fig 4)
Also look at Diaboloes; (fig 5) they are also interesting.
One can color tiles alternating colors if each vertex has an
even number of cells touching it.
Not going to talk about dual graphs. ``The dual graph is
bipartite.''
The Dimer Problem.
Look at the dual correspondence between tiles and Dimers in
figures 6 and 7. In Fig 6, we need to connect triangles that
share edges to form lozenges.
In Figure 7, we need to find a dimer configuration such that each
vertex is paired with exactly one neighbor.
Pick a random configuration: notice that once you make a few
decisions, others are forced upon you. (Fig 8)
Now convert it back to lozenge tilings. Suddenly, we see a 3-d
cube figure! (Fig 9) Figure 10 shows positive and negative
directions.
Now Boytcho produces a double die so that we can see a cube within
a cube.
Let height be defined as h(x,y,z) = x + y + z
Figure 11 shows the height of each vertex.
Figure 1 shows Abe's 2-d analog, so we understand what height
really means. In this figure, the line x+y=0 represents height=0.
The point (1,2) has height=3. Its ``real'' distance from the
h=0 line is 3/\sqrt{2}. But we like integers!
Now we need to mathematically define a way to calculate what your
eye sees as height.
Height

Imagine moving along the edges of the shaded triangles of figure
13. If it is shaded on your left, increment your height by one.
If it is unshaded on your left, decrement your height by one.
This way we generalize what a height function is. We can define
the height of a vertex on a domino graph by analogy to
lozenges. (Fig 14)
On a square, the boundaries must be alternating zeros and ones on
top and bottom, and alternating zeros and minus ones on left and
right. Boring.
But on an Aztec Diamond of order 3, the height goes up from 1 to
7 as we go from left to top, then back down and up as we go
around the other sides. (Fig 15)
These different boundary conditions change how the inside behaves.
The Aztec diamond is approximately a saddle shaped surface.
That's why the corners freeze out.
You can think of a large lozenge hexagon as a monkey saddle.
All six corners freeze out, leaving a circular area, like
figure 16.
Assignment:
(1) Count the number of Domino tilings for 2xN rectangle,
for n<=10. There is a pattern there. Find it and exploit it.
(2) Find all domino tilings of Aztec Diamond of Order 2.
See figure 17. Find all height functions. Look at several
Order 3 Aztec Diamonds, with height functions. Try to figure
out what heights can occur at the different vertices of an
Order 3 Aztec Diamond.
SSL Minutes
8 Feb 2001
Abe & Nick
Geir brings beverages next time.
Abe S. and Nick P. took notes.
There was an error on pg 13 of "Generalized Domino Shuffling." The
Fortress, which is labeled order 3 is actually order 4.
A point on rules of order: We should be patient in answering questions
so that a higher proportion of the group can absorb and contemplate
the questions. There's no reason anyone should get lost. Also, keep
anecdotes under control.
Next Thursday or the Thursday after, Jim will meet with us one-on-one.
Also, as for the time sheets, hours are like electrons: i.e.,
indistinguishable. It doesn't matter to Jim what you right on the
sheets as long as the total number of hours is correct.
We will be put on Domino and Bilinear email lists.
We were given a handout. We should be able to read sections
1,2,3,6,7,8 reasonably well.
Regions With Holes:
Take a 6x6 square with the middle 2x2 hole missing.
The height function is definable as long as the missing region is
tileable. However, 2x2 block rotations can not be used to change the
tile configuration.
David Wilson has done work on Aztec Windows. Search for it if you
are interested.
Homework:
Abe (me) discussed his (partial) solution for
counting the tilings of a 2xn rectangle with exactle k verticle tiles.
He noted that N(n,k)=N(n-1,k-1)+N(n-2,k)
By using induction on N and K, the following formula can be found:
N(n,k) = C( n+k/2, k);
where C(a,b) is the binomial coefficient (combination) function.
New Stuff:
Counting lozenge tilings on a semi-regular hexagon, sides of length
a,b,c.
The number of tilings,
H(a,b,c) = Product_{i=1..a, j=1..b, k=1..c} ((i+j+k-1)/(i+j+k-2))
New Homework:
1. Prove that H(a,b,1)=C(a+b, a) (i.e., (a+b)!/(a!b!) )
2. Use domino Shuffling to prove that H(2,2,2)=20.
Other:
Undergraduate Research Seminar volounteers:
Kristin, Rachel, Nick?, Abe?, Pavle
As for X-forwarding in B107, we don't know how to fix it.
That is all!
SSL Minutes
13 Feb 2001
Rachel
Jim asked us what we plan to do after graduation. Most of us plan to go to
graduate school at some point in our lifetime.
Then we went over our homework. Pavle gave a cool algebraic proof for our
first problem, that Jim noted was a telescoping sum and further simplified.
Domino Shuffling and Hexagon Matchings
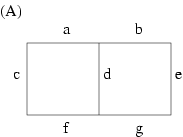 There was a longer discussion over our second problem, using domino
shuffling to prove that H(2,2,2,) = 20. The claim in the paper is, in
order to count perfect matchings of these tiled hexagons, first "flatten"
them into square grids, and then count. Give each matchings weights for
example, for this graph (Figure A) we have cde + aef + bcg. Give weights
of zeroes and ones, with zeroes to the vertical edges so that they don't
contribute to the sum.
There was a longer discussion over our second problem, using domino
shuffling to prove that H(2,2,2,) = 20. The claim in the paper is, in
order to count perfect matchings of these tiled hexagons, first "flatten"
them into square grids, and then count. Give each matchings weights for
example, for this graph (Figure A) we have cde + aef + bcg. Give weights
of zeroes and ones, with zeroes to the vertical edges so that they don't
contribute to the sum.
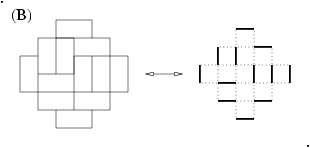 Boytcho had a question about how do we fit these flattened hexagons into an
Aztec diamond graph? NOTE: there IS a difference between an Aztec diamond
and an Aztec diamond graph! (my name is gecko, not to be confused with
geico, which can save....) See Figure B as an example to differentiate
between the two.
Boytcho had a question about how do we fit these flattened hexagons into an
Aztec diamond graph? NOTE: there IS a difference between an Aztec diamond
and an Aztec diamond graph! (my name is gecko, not to be confused with
geico, which can save....) See Figure B as an example to differentiate
between the two.
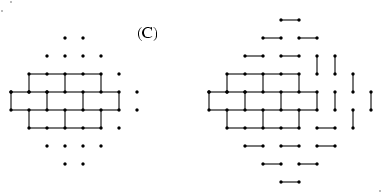
Boytcho's question further asked, what weights would you assign to the
flattened hexagons when trying to fit them into the Aztec diamond
graph? Jim showed examples where it does and where it does not work to fit
them in. Basically you must match the inner graph with the outer
graph. See Figures C1 (not able to fit it into an Aztec diamond graph of
order 4) and C2 (are able to fit it into an Aztec diamond graph of order
5). In C2, where the fitting DOES work, note the matchings that were NOT
forced; there are only four possibilities between these, hence the
"conclusion: the sum of the weights of the matchings of the graph is equal
to four times H(2,2,2,)".
Jim explained and gave two examples of the reduction algorithm. This
algorithm is shown in the domino-shuffling handout, but Figures D1 and D2
show the step-by-step process of the examples that Jim explained. The
second example is with a simple crushed hexagon to aid us with our
homework. The basic procedure is to star every other cell, switch opposite
weights on each cell, divide by the cell factors, erase the outer edges and
then start the procedure over again. Finally you multiply all the cell
factors and voila!; you wind up with the number of perfect matchings of the
original graph.

We ended our session with Jim asking about a previous homework assignment,
basically that we find questions and ideas about the Project Summary
handout. We went around in a circle and these are the questions we listed
(the questions that Jim answered have answers succeeding in square
brackets, other questions to be answered in the future!):
What should we do?
"What should we do?" [Read Sections 1, 2, 3, 4 of the generalized shuffling
handout; read the entirety of the grant proposal; start programming if you
can, programming neophytes should work on manual calculations; think about
what other types of programs we want or need?]
Ergodic theory?
Positive and zero entropy regimes?
Will non-programmers be able to contribute? To whom can they talk?
['Computer mentors' such as Abe, Hal, Boytcho; also we can use our funding
to purchase reference books for example, for programming.]
Pfaffian method?
When do we start? [Now! See Figure E and think about patterns, in this
theoretical example and in examples of your own. In programming/coding,
look for patterns!]
Aztec circle?
Role of wild ideas?
What should Hal program? (What should we program?)
Finally for all you vegetarians out there, Jim noted that cochineal extract
is extracted from bugs, so if you plan to be a pure vegetarian, it is
recommended to look for mosquito extract on fruit juice ingredients
listings before you partake! (Thanks so much! Someday I will have so many
things on my list of what NOT to eat that I will just constantly be
spooning up tofu! How exciting!)
SSL Minutes
15 Feb 2001
Boytcho
 avle will be the Beverage Person for Tuesday next.
avle will be the Beverage Person for Tuesday next.
 achel said something about brownies.
achel said something about brownies.
Intro to Ergodic theory
This is a theory which studies measurable dynamical systems. Being
measurable means that said systems are probabilistic.
If we throw a coin repeatedly we can talk about the probability of a sequence
of events. For instance
Some Markov Chains also exhibit ergodicity. A simple MC is for
instance: If it rains today then 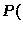 it will rain tomorrow
it will rain tomorrow
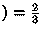 ,
and if it is sunny today then
,
and if it is sunny today then 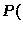 it will be sunny tomorrow
it will be sunny tomorrow
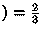 .
.
The above examples have one dimensional time, but that need not necessarily
be the case with ergodic systems. We can have two (, three, &c.)
dimensions of time. For example see the domino tiling in fig 1.
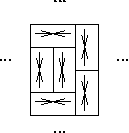
Here we use  to denote one of four possible states. The system
depicted above has some built in restrictions. A
to denote one of four possible states. The system
depicted above has some built in restrictions. A  state can only
be to the left of a
state can only
be to the left of a  square. A
square. A  state can only be under
a
state can only be under
a  square.
square.
An Interesting Question is: ``How random can a system be with
restrictions such as the above?''
- Entropy is a measure of randomness.
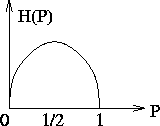
The figure above illustrates entropy (denoted traditionally by  for some
reason), in the case of a coin. If the coin is biased so that
for some
reason), in the case of a coin. If the coin is biased so that
 , then there be no randomness, thus
, then there be no randomness, thus  . If the coin is
fair, i.e
. If the coin is
fair, i.e
 then we have maximum entropy.
then we have maximum entropy.
If we are taking measurements of a sequence of events (say repeated tossings
of a coin) at the rate of one measurement per unit of time, the most randomness
we can hope for is 1 bit per unit of time.
Then there was a brief discussion of Independent Identically
Distributed events. The author of these notes is not quite certain, how to
tie that in with the rest of the discussion, yet it seemed relevant enough to
be mentioned.
of a one dimensional system is the 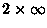 square grid
tiled by dominoes. A piece of it is shown in the figure bellow.
square grid
tiled by dominoes. A piece of it is shown in the figure bellow.

In this case a restriction is that 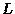 and
and  states must be next to each
other in the correct order. (There are exactly two tilings that we are
neglecting here for their negligably low probability of occurring. Those are
the two ``brick-work'' tilings).
Here we prefer to use
states must be next to each
other in the correct order. (There are exactly two tilings that we are
neglecting here for their negligably low probability of occurring. Those are
the two ``brick-work'' tilings).
Here we prefer to use 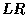 for horizontal dominoes
as opposed to
for horizontal dominoes
as opposed to  , for this makes it a local rule, and makes it easier to
verify if a piece of the tiling is correct. It takes a while to check if
a long sequence of
, for this makes it a local rule, and makes it easier to
verify if a piece of the tiling is correct. It takes a while to check if
a long sequence of  s is of even length.
s is of even length.
So a question we want to answer is how random can a piece of that strip be?
If we start somewhere on the strip we want to know how likely are we to
see 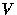 in the next column as opposed to
in the next column as opposed to 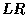 ?
?
One way to make a random system of this kind is to
use a biased coin to decide whether to put down a 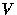 or an
or an 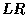 . If the
bias-ratio is too close to
. If the
bias-ratio is too close to 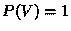 (always
(always 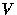 ) or
) or 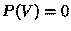 (always LR),
the system will have low entropy. It has higher entropy when the bias is
(always LR),
the system will have low entropy. It has higher entropy when the bias is
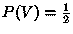 (a
fair coin), but this is still not the best choice. It turns out that
the choice of bias that leads to the highest possible entropy is
(a
fair coin), but this is still not the best choice. It turns out that
the choice of bias that leads to the highest possible entropy is
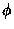 (aka The Golden Ratio).
(aka The Golden Ratio).
There is a close relationship between the Golden Ratio and Fibonacci numbers,
namely
in English: The ratio of two successive Fibonacci numbers approaches 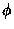 .
.
Now we can think back to the first homework for some insight on why this is
a good bias for this particular coin.
Consider a 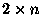 piece of the strip. The first column of it can be
piece of the strip. The first column of it can be 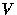 or
or 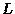 . If it be
. If it be 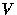 we have a
we have a
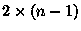 piece to tile, otherwise the
untiled part is
piece to tile, otherwise the
untiled part is 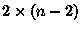 . As we have seen the probabilities involved are
related to the Fibonacci numbers.
. As we have seen the probabilities involved are
related to the Fibonacci numbers.
Hal has seen matrices related to a similar system.
we can think of covering the plane with
dominoes. One simple way to go about that is to divide the plane in 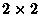 pieces and use a fair coin to tile each of these pieces. We then have 1 bit
of information to each
pieces and use a fair coin to tile each of these pieces. We then have 1 bit
of information to each 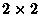 , therefore
, therefore 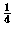 bit per square.
And we can do much better than that.
bit per square.
And we can do much better than that.
If we take a random tiling of a 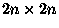 square with dominoes, the
probabilities of what domino covers a square in the inside are very much the
same as they are in the
square with dominoes, the
probabilities of what domino covers a square in the inside are very much the
same as they are in the 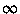 -plane. We can ask for instance how likely
are we to come across three horizontal dominoes, stacked one on top of another
in a
-plane. We can ask for instance how likely
are we to come across three horizontal dominoes, stacked one on top of another
in a 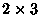 . The situations would again be similar on a large
. The situations would again be similar on a large 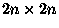 and
the entire plane.
and
the entire plane.
If we take however and Aztec Diamond, things go terribly wrong really fast.
In the polar regions for instance the probabilities are skewed at places that
are much further away from the border than in the simple square case.
In the very center of the Aztec Diamond, we have the max entropy.
We can use the Generalized-Domino-Shuffling ( ) algorithm to find the
probability of a stack of three h-dominoes by finding the number of matchings
of a graph depicted below.
) algorithm to find the
probability of a stack of three h-dominoes by finding the number of matchings
of a graph depicted below.
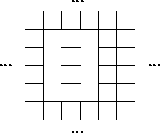
If we chose to leave all the edges between the six vertices of interest
as to simplify the 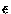 calculations in
calculations in  , we would increase
the number of matchings by a factor of
, we would increase
the number of matchings by a factor of 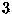 .
.
In the Aztec Diamond, the polar regions are 0-entropy regions, whereas the
temperate zone is of positive entropy.
If we travel from the center of the Aztec Diamond towards one of the poles,
at about 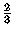 of the way the probability of having a ``north''
domino approaches
of the way the probability of having a ``north''
domino approaches 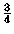 .
.
Another phenomenon that may occur is ``Hole in The Wall''. This is a rectangle
of even width, which if it is shaded in standard checkerboard fashion,
has the white squares from the leftmost column and the shaded squares from
the rightmost column removed. In other words, the sizes of consecutive rows
alternate between 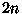 and
and  and the rows are centered left to right.
Such an animal has an unique tiling by dominoes.
and the rows are centered left to right.
Such an animal has an unique tiling by dominoes.
The point of this is, that we may achieve the behavior of the sub-arctic
region of an Aztec Diamond on a square if we remove the right pieces from the
border.
Then we talked about halved Aztec Diamonds, and lattice paths in them, which
force tilings.
Then Prof. Propp addressed a question by yours truly having to do with
the basic moves on a Diabolo-tilable region. An appropriate illustration
of the graph that we would want to match can be seen on p.10 of the  paper. The graph which consists of octagons and squares. The point is
there are TWO basic move in the Diabolo world, one deals with the two matchings
of a square, the other with the two matchings on an octagon.
paper. The graph which consists of octagons and squares. The point is
there are TWO basic move in the Diabolo world, one deals with the two matchings
of a square, the other with the two matchings on an octagon.
The question was raised as to how to get a text file to fit predetermined
line lengths in UNIX, which brings us to The UNIX Command of the Day: fold(1).
SSL Minutes
20 Feb 2001
Hal and Nick
Misc.
We were missing a couple of SSLers including
Rachel, who was supposed to bring brownies. And we had a new guy,
Joel. Hi, Joel.
There will be an "open bar" in the hallway on Thursday. We will drink
up the excess beverages.
Clarification of previous notes:
Original: "maximum entropy is found at very center of Aztec Diamond"
Revised: there may be "bad spots" near center, but they'd be small enough to
be negligible.
Why: Entropy is a statistical property, and we look at a small
statistical region at the center of the diamond. If there is a bad
spot, it is *statistically* small. Is that clear enough while
still being accurate?
On Thursday, everyone will meet individually for 10-minute with Prof.
Propp and Mike. A schedule has been devised. In the other room, we
get to play on the computers and Abe will talk about *nix OSes and
programming, the Hal will talk about his program.
Is everyone caught up on reading? Hal is not. Jim said that that can
be a good thing, as long as you ware working on something else and
asking good questions. For example, the "tilability question," or
Boytcho's "Is there an analog to domino shuffling for diabolo
tiling of a fortress?"
What are sticky points on the reading? "Why Generalized Domino
Shuffling called GDS?" Also, someone asked about the notation in one
of the papers.
ASMs and Domino Tilings
A domino tiling of an AD can be described with a height function and put
into a matrix.
N nN nN = a north pointing domino
E N wEnN
W E E == wWeEwE Ss = a south pointing domino
W N W WnNeWe
S S SsSs E = a east pointing domino
S Ss e
w = a west pointing domino
W
In this picture, capitol letters represent black squares on a
chess board and lowercase letters represent white squares.
Obviously it is only necessary to enumerate which domino is the
black tiles.
This is how Hal's been thinking about it, because that's how his
program runs.
This example takes even diagonal groupings:
A=(0 2 4 6 8
2 4 6 4 6
4 2 4 2 4
6 4 2 4 2
8 6 4 2 0)
multiply it by one-half (A*.5):
A=(0 1 2 3 4
1 2 3 2 3
2 1 2 1 2
3 2 1 2 1
4 3 2 1 0)
convert to ASM ('-' means "-1") of size (n+1)x(n+1):
A=(0 0 1 0
1 0 0 0
0 1 - 1
0 0 1 0)
Here's the ASM of the other (odd) diagonal grouping:
B=(0 1 0
1 0 0
0 0 1)
...which is a nxn permutation matrix.
Algorithm to convert matrices made from AD's into ASMs:
Given submatrix
C=(a b
c d)
ASM entry = { 0 if a+d=b+c , 1 if a+d=b+c-2 , -1 if a+d=b+c+2 }
Definition: ASMs are compatible if, when the small and large ASMs are
converted to AD's, adjacent vertices differ by 1 or 3.
Question: For a given nxn ASM, how many compatible
(n+1)x(n+1) ASMs are there?
Question: For a given (n+1)x(n+1) ASM, how many compatible
nxn ASMs are there?
Number of positions free to change in smaller array is sum of "-1"'s in
larger arrays ASMs.
Claim: An (n+1)x(n+1) ASM with k -1's is compatible with exactly 2^k
nxn ASMs.
Claim: An nxn ASM with j +1's is compatible with exactly 2^j
(n+1)x(n+1) ASMs.
Plot the locations of -1's in an ASM, and it might look like a circle, we
think.
Bonus Questions:
(1) Show number of tilings of an order n AD that do not contain ``bad
local conditions'' is equal to number of order n Baxter permutations.
(2) Prove the conjecture: the # of ASMs of order n that link up
terminals as 1 to 2, 3 to 4, ..., (2n-1) to (2n) is exactly equal to
the number of ASMs of order n-1.
Note: a -1 in the (n+1)x(n+1) represents something. ???
The Square Ice Model
0 + 0 0 0 1 2 3 4
+ - 0 + ==> 1 2 1 1 3 ==> to the flux ==> rotated to get
0 0 + 0 2 1 2 2 2 line vector densly packed
0 0 0 0 3 2 3 3 1 field. flux line field.
4 3 2 2 0

I need a good explanation of what is going on here! Can anyone help?
Matrix to Vector Field
each entry of the matrix coresponds to a node, and neighboring nodes have an
edge in the direction of the one of which the coresponding entry in the matrix
is bigger.
Vector Field to Square Ice
Take each edge and rotate it by -90degrees ('-' here means clockwise.)
The center of each square from the vf is now a node in the si picture.
Square Ice to Densely Packed Flux
Take the nodes of the si and color them chessboard-wise. Now look at the shaded
nodes. The edges that go AWAY from a shaded node we shall color blue and the
arrows that go INTO a shaded node we shall deem red. And then omit the
directions for the dpf picture.
When looking at the dense flux line graph of an ASM, with, say, 12
terminals, (numbered 1 - c) the number of ways to connect terminals 2
& 3 is equal to the number of ways to connect 3 & 4.
This theorem was proved by Ben Wieland.
1 2 3
c
4
b
5
a
6
9 8 7
Publishing:
There are three potential articles we have lined up:
- Properties of tilings of different regions
- Baxter permutations and domino tilings
- Blue/green tilings
SSL Minutes
27 Feb 2001
Dominic and Rachel
**Note: I apologize in advance if I did not understand/record your main
points you presented on Tuesday. If I missed anthing, misinterpreted what
you said, or said something you did not say, please send me a note
explaining the mistake or what you would like changed.
Hal will bring the beverage for Thursday's meeting.
Kekule structures from benzene molecules are related to Hal's interest in
nanotubes and their possible tilings. A benzene molecule yields 2 Kekule
structures (2 perfect matchings).
Question: Do we want our meeting minutes in postscript or pdf?
We will collect the minutes of all our meetings into a separate file.
It is a good idea to send out both rough and revised versions of the
minutes. When revising minutes, though, send the addenda/errata and the
full revision in separate messages. That way, people can immediately see
what has changed from the rough draft, but also have a revised text to
refer back to at a later date. Also, multiple revisions are allowed and
even encouraged. Everyone can suggest changes, and the authors implement
them.
Additionally people questioned how "good" should the minutes be? and should
there be a difference in the quality of notes sent by Tuesday notetakers vs
Thursday notetakers? The revision version of the notes should be as
'perfect' as we can get the notes, and that's how 'good' the notes should be!
We went around the room, and each person conducted the meeting for roughly
five minutes.
Geir: Nothing in particular. Not so much interested in the Arctic Circle,
but in the number of matching permutation matrices. Interested in Baxter
Permutations. What are they?
**Homework assignment for Thursday: Find a definition of Baxter Permutations.
Abe: Concerned about the number of ways to join 1 & 2, 3 & 4, etc. Also
interested in symmetries in blue/green paths used to join these
numbers. Boytcho was also interested and had been working on these
blue/green path symmetries as well.
Pavle: Interested in the tilings of a square (or diamond, depending on
which way you look at it). Presented a few pictures to explain his ideas,
and showed how he has been spending his time.
Dominic: Wondered why David Robbins tried to make his data look similar to
Pascal's Triangle. It turns out Pascal's triangle can also be applied to
Aztec Diamonds. Other than that, Dom has been spending most of his time
reading the articles and learning computer language.
Nick: Opted to speak at the end of the meeting because his talk would
probably take longer than 5 minutes. However, we did not have enough time
at the end of the meeting for him to talk.
Joel: Has mostly been catching up. Interested in overlapping domino
matchings, blue/green paths, and how they are related to superpositions of
domino tilings.
Michael: Ceded his time to others.
Dan: Wonders if there's a good source to learn Java. Computer-literate
people suggested taking Computer Science 368 here at the
university. Also, perhaps read through a few Java books, and within a few
minutes of reading, you should be able to tell if it fits your learning style.
Winston: Interested if there's research done in the tilings of any regular
polygon. Jim showed the example of a regular octagon (edge length 1) being
tiled by 2 squares and 4 non-square rhombi. There is no known way to tile
a 2n-gon (I think). Also, Jim introduced ribbon tiles. There are two
2-ribbons. One looks like a horizontal domino. The other looks like a
vertical domino. There are four 3-ribbons. They look like the Tetris
pieces generated when one can only move eastward and northward. How many
ways are there to tile a figure using ribbon tiles?
Rachel: Interested in having brainstorming sessions. Also concerned about
what/how an SSLer without mathematical sophistication can contribute.
Interested in having a study session, which could be facilitated if all
members could post a list of their free times. The group decided it could
be beneficial if a member specialized in one specific area, so even if
he/she did not have mathematical or computer sophistication, he/she could
teach others about his/her area of expertise.
Boytcho: I apologize, but I'm not exactly sure how to put this into
words. He looked at all the different tilings of an order-2 Aztec Diamond.
Then he translated each tiling into a 4-by-matrix. Then he transformed
this into an arrangement of green and blue lines, assigned a "weight" to
each colored segment, and looked for patterns.
Kristin: Has spent her time learning about computers. Interested in
tiling different polygons. Can we use other shapes (which ones?) for
tilings? When do you know if a region is tilable? Jim explained the
marriage lemma and its connection with tilable/untilable regions.
Hal: Comments on the ideas Boytcho presented. He represents Aztec
Diamonds as huge arrays. Interested in how we can go from a Aztec Diamond
to any other shape. Hal's time also ran out and he will be given time at
the next meeting to finish his minutes.
Figures will be added in the revision to these notes.
SSL Minutes
1 March 2001
Hal and Boytcho
People have things to say
Boytcho says that Mathematical Induction works for any well
ordered set, such as the positive integers or the Cartesian product of
a finite number of well ordered sets under the dictionary ordering.
Someone forgets that the real numbers are not well ordered.
Hal asks what functionality should go into the program. He
gets good feedback:
- Detect large chunks of same type of block (aka icebergs)
- Calculate Height Functions
- Add together two ADs (Eric Kuo's algorithm)
- Interactive and non-interactive modes.
- convert to ASM (in real time)
- Give lots of power to the interface.
Nick talks about how he's given some thought to representing
a DPF (Dense Packed Flux). Example :
o---o---X---o
| | X |
XXXXXXXXX---o 4 6 8
| | | | ==> 1 5 4
o---XXXXXXXXX 2 9 1
| X | |
o---X---o---o
Each square is represented by a bitwise numbering system:
1
o---o
8 | | 2
o---o
4
Crash-course-type Intro to the Binary Number System: Traditionally humans
use the symbols 0, 1, 2,... 9 to write numbers down. These are the ten digits.
On those symbols is based the decimal (aka ``base ten'') number system.
When we write down a number say 935, that means that the magnitude of it is
obtained by the following formula
9*102 + 3*101 + 5*100 = 900 + 30 + 5.
The position of each digit represents the power of ten that it is a coefficient
for. We need exactly ten symbols for the base-ten representation of numbers to
avoid a mess and have a unique representation for each number. Ten is a
convenient number base for humans to work with, but not so for computers. They
deal better with numbers represented in binary (base two). The symbols
used are 0 and 1. (Traditionally to avoid ambiguity a subscript is used to
indicate the base.) A binary number is 10012 for example. This is the number
1*23 + 0*22 + 0*21 + 1*20 = 910. The word digit is related to
the decimal system in that it means one of the ten symbols used in it.
Therefore with binary numbers we talk of bits (from Binary digIT).
The numbers chosen by Nick above are all powers of two, which means that they
have exactly one bit in their binary representation set to 1. Computers can
easily be convinced to deal with numbers bit by bit. Another advantage of
that choice is that the sum of the numbers corresponding to the ``on'' sides
of a square never exceeds four bits, and its binary representation makes it
immediately obvious which sides are ``on.''
Add together the numbers of those sides that have flux lines on them.
Then you get a nice matrix.
You can flip a square if it is a 5 or a 10. Let's flip the 5 in the
center of the matrix to a 10. This affects the four squares adjacent
to it. Legal moves:
5 to a 10: 10 to a 5:
-4 +4
+2 +5 +8 -2 -5 -8
-1 +1
Then we get:
o---o---X---o
| | X |
4 2 8 XXXXX---X---o
flip--> 3 10 12 ==> | X X |
2 8 1 o---X---XXXXX
| X | |
o---X---o---o
Software
We get volunteers to look at redblue.c: Nick, Hal, Boytcho,
Rachel. (http://jamespropp.org/hidden/ssl/blue-red.c)
We also need to find out what other software is out there: Abe, Nick.
Baxter Permutations I (Boytcho)
Let N be an odd element of the Natural Numbers.
Let IN = {1, 2, 3, 4, ... N}
Let ON be the odd elements of IN.
Let EN be the even elements of IN.
Definition: P is a Baxter Permutation iff
- P(ON) = ON
and P(EN) = EN
- if P(n) is between P(2i) and P(2i+1) then n >= 2i
- if P(n) is between P(2i) and P(2i-1) then n<= 2i
Baxter Permutations II (Mike)
The set of permutations on In is called Sn.
If w is an element of Sn, w is Baxter iff for every
i in {1, 2, 3, ... n-1}, it passes the test.
The Test. Let r = w-1(i).
Let s = w-1(i+1).
Assume r > k.
If there exists a ki such that,
for all t in [k,r], w(t) <= i and,
for all u in [s,k], w(u) > i, then the test is passed.
Here's a case by case run down:
- If s < r Then we ask is there a k in [s, r] for which we know that
P(s), ... P(k) are all <= i, and P(k+1),\dots P(r) are all > i?
- If r < s Then we ask is there a k in [r,s] for which we know that
P(r), ... P(k) are all > i, and P(k+1), ... P(s) are all <= i?
- It is never the case that s = r.
Here is an example: we permute (1,2,3,4)--> (2,4,1,3). For i=1 we can
partition in the following way 2,4,| 1. So we don't know yet this not
to be a Baxter permutation. For i=2 we cannot however partition
2,4,1,3
in
a way that would satisfy our question, thus we now know the permutation to not
be a Baxter Permutation.
ASMs and Monotone Triangles
There is a nice correspondence between ASMs and
Monotone Triangles.
0 1 0 0 0 0 1 0 0 0 2
1 - 1 0 0 1 0 1 0 0 1 3
0 0 0 1 0 <--> 1 0 1 1 0 <--> 1 3 4
0 1 0 0 0 1 1 1 1 0 1 2 3 4
0 0 0 0 1 1 1 1 1 1 1 2 3 4 5
ASM Intermediate Monotone Triangle
In each entry of the intermediuate matrix, add up the
entries of the ASM going down the column until you get
to the corresponding location. In other words,
the (i,j) (row, column) entry in the
intermediuate matrix is simply the sum from k = 1 to k = i of the
(k,j) entries in the ASM.
Note that the rows of the intermediate matrix add up to
(1,2,3,4,5)T.
Now, we ask the question: ``For each row of the
intermediate matrix, which columns hold 1's?'' The answer to that is
the monotone triangle.
Properties of the monotone triangle (MT).
B
A <= B / \ B <= C
/ \
A-----C
A < C
Usefulness: It is easy to generate MTs. (bluered.c)
Plane Partitions and Semi-Strict Gelfand Patterns
What is a partition of a number? A set of positive numbers that
add up to it. 10 = 6+4 or 10 = 5+3+2.
Partition Ferrer's Diagram
5 .....
3 --> ...
2 ..
A Plane Partition has a three dimentional graph, not a 2
dimentional graph. Here's an example Partition:
3 2 1 1 2 3 7 8 9
2 1 --> Boxes in three Space. --> 1 2 4 7 8
1 2 5 7
1 3 6
1 4
1

Stack them as boxes inside a cube. Then think of that cube as
equivilent to a hexagon tiles with lozenges. Draw that. Then extend
the cornes out, as shown in the graph. Number the vertically oriented
lozenges based on the distance from the line on the left side.
Transfer the numbers into a triangle. That's a Semi-Strict Gelfand
Pattern.
Properties of the Semi-Strict Gelfand Pattern:
A < C
A-----C
\ /
A <= B \ / B < C
B
Why was that important?
SSL Minutes
6 March 2001
Abe and Joel
Sorry, Guys, I forgot about this... It was the week before spring
break, so I must've gone brain-dead immediately afterward.
For the record, Joel had his version of the notes to me
promptly... I'm the slow one.
I.
Jim gave a brief discussion on cyclic permutations and groups:
Transformations in the group MUST be rotations in the plane, not
reflections or anything else.
There was a discussion of this applied to rhombus tilings, which I
won't even TRY to draw in ASCII. Rotations in this case can only be
rotated 120 degrees, giving an orbit of order 3.
Say there are m tilings that are invariant under cyclic permutations
and 3n tilings that aren't. The total number of permutations would be
m+3n. Removing the redundant ones would give m+n, which is unlikely
to have a nice answer.
A usual question: "What is the number of ... up to symmetry?"
Changing symmetry can often simplify equations. Additionally,
transformations can be paired, etc.
II.
Another topic: Dense packing models of hexagon grids. Someone might
want to look into this, as no one has investigated it yet.
III.
Notes on programming: IT may be more efficient to make straightforward
programs without worrying about nice ways of packing bits and so
forth. This will make modification and extension easier.
IV.
Coupling from the Past: It is difficult to generate a random ASM from
scratch, but by repeatedly permuting in a random fashion, it will
eventually reach something close to a uniform distribution. Coupling
from the past is a method which is proven to accelerate this
convergence.
V.
Question:
What about convex hulls around a set of points? How close is it to a circle?
VI.
ASMs/TOADs:
How does one create a dense packing from a TOAD?
1. superimpose two ASMs for TOAD
2. Turn these into Blue-green maps
We need some representation for TOADs and ASMs that will allow easy
cycling through all variations. Semi-strict Gelfand
Patterns are good
for this application as they are easy to generate.
Date: Thu, 29 Mar 2001 22:59:54 -0600 (CST)
From: propp@math.wisc.edu
To: ssl@math.wisc.edu
Subject: correction to Notes for March 6
The notes for March 6 say:
>We need some representation for TOADs and ASMs that will allow easy
>cycling through all variations. Semi-strict Gelfand Patterns are good
>for this application as they are easy to generate.
"Semi-strict Gelfand Patterns" should be replaced by "Monotone Triangles".
Remember, Semi-strict Gelfand Patterns correspond to plane partitions;
TOADs and ASMs correspond to monotone triangles. (Leastaways, ASMs
correspond to monotone triangles; TOADS correspond to something a bit
more complicated.)
Jim
technique:
generation => convert to matching => examine
N is a function
\sum_A (1^{N(A)}) = number of ASMs
\sum_A (2^{N(A)}) = number of TOADs
\sum_A (3^{N(A)}) = number of nice function for some product formula?
\sum_A (4^{N(A)}) = UGLY (until nontrivial formula is proven)
Nice weighted product formulas are also important at times.
Next Time:
Q analogs and
P-adic (P is prime)
that's all.
SSL Minutes
8 March 2001
Kristin and Nick
Jim requested that someone pick up an article that is in the Physics
Library: Baxter, Kelland and Wu: J. Phys A_9, 397 (1976)
Jim also requested that we work on determining how to mutate a grid diagram
by local moves in order to get all other possibilities.
Geir explained how to use q-analogs.
He explained this in relation to lattice paths.
Start with a grid and by moves of only down or to the left, go from upper
left vertex to lower right vertex.
How many paths are there?
A way to represent the answer is to consider the area underneath the lattice
path and encode the info with a polynomial in q.
The coefficient of q^i equals the number of lattice paths with an area of i.
So, in the example of a 2x2 square grid, the number of lattice paths can be
given by: 1+q+2q^2+q^3+q^4.
Next Geir defined [n]=(1-q^n)/(1-q)=1+q+q^2+...+q^(n-1)
He went on to define [n]!=[n][n-1][n-2]...[2][1] and you can substitute for
[n] in terms of the q notation previously defined. [n]! is called a
q-factorial. This allows us to define q-binomial coefficients, which are
analogous to the standard coefficents, but with the bracket notation. So,
the q-binomial coefficient looks like this:
[n]!/([n-k]![k]!)
This can be applied to the example of the 2x2 grid, where the number of
lattice paths is given by [4]!/([2]![2]!) And Geir worked this out and
verified it.
So, in general, on the kx(n-k) grid, you use the q binomial coefficient to
determine the number of lattice paths.
Why is this useful? The q-analog gives more useful information. For
example, it allows you determine how many paths there are for a given area
under a path.
This can also be applied to the lozenge tilings of a semiregular hexagon
with sides (a,b,c). We have a formula that tells us the number of tililings
of such a region, which is the triple product of the quantity
(i+j+k-1)/(i+j+k-2).
If we think of the three dimensional picture of cubes in a box that the
hexagon tiling represents and take the triple product of
[i+j+k-1]/[i+j+k-2] we get the number of cubes.
Jim went on to explain how q-analog can also be applied to the number of
tilings of an aztec diamond. I am a little fuzzy on this though and Nick
did not have much in his notes about this either.
Next we went next door and Hal showed us his really beautiful applet and Jim
showed us another program which I do not know the name of and could barely
see. There was also a 'tripped-out' program that was run for us.
SSL Minutes
20 March 2001
Dan
(someone?) is working on proving that the larger matrix in the ASM
representation of an order "2" (n) aztec diamond is the smaller
matrix in the order "3" (n+1) ASM after doing domino shuffling.
Jim pointed out that "pushing down" the height in an aztec diamond is
equivalant to adding [1, -1; -1, 1] to the ASM.
(Hal) proposed the idea of looking at ASM hieght functions with the
minimum height fuction subtracted out of them to see if the
properties were interesting.
Some ideas for the fair were tossed around, including displaying Hal's
java program, and explaining various things we're working on, such as
the Baxter conjecture and the blue-green model conjecture.
Jim explained one of the properties of compatable ASM pairs. Each ASM
is compatable with 2**[number of -1s] smaller ASMs and 2**[number of
1s] larger ASMs. Each item can be represented as one item in an
ordered postset, where each order of ASM represents one level of
depth. By taking a random path from the bottom up you can generate a
random pair of compatable ASMs. However, you need to use some sort of
weighting to generate a random ASM because picking a random path will
favor ASMs with more -1s
Geir showed that you can quickly convert between an ASM to a densely
packed flux line model by going straight on 0 and turning on -1/1
SSL Minutes
22 March 2001
Pavle
What we did
We spent most of our time in the computer room, each doing a small project.
Hal was working on the heaxagon version of blue-red. That is, it will do
for hexagonal tilings what it does for rectangular ones.
Joel was working on the probability of finding a 1 or -1 at a certain spot
in a NxN ASM as a way to see if there is any way to get a circle, the likes
of which we see on an Aztec diamond.
Pavle was working on figuring out a good algorithm to figure out which
(N+1)x(N+1) ASM was compatible with which NxN ASM.
Geir and Kristin were computing the number of ASM's of N=1, 2, . . ., 8 to
see how many of them connected 1 with the point futhest away on a tiling.
Dominic and Nick were doing research on baxter permutations, and trying to
make a program that would let them know, for an input sequence, whether it
was a baxter permutation or not.
Boytcho and Abe were working on figuring out a way to store a large quantity
of numbers. Boytcho then pointed out that you can't store 20! numbers in
less than a supercomputer, so that idea was shot down.
Dan looked at ASMs and the DPFL model. Also looked at the hex flux line
model thingy.
SSL Minutes
27 March 2001
Dominic and Hal
Etcetera
Jim has assumes responsibility for spending the interest off of a $5000
endowment that a former undergrad has given the department to be spent
on games. Any ideas? By the way, 5% of $5000 is $250.
Joel will bring the beverage for Thursday.
Undergraduate Research Symposium
The Undergraduate Research Symposium (URS) is quickly approaching. We
need to decide what we will all have at the URS. We generated a rough
list of topics, people responsible for different topics, and materials
we need:
Topics
- TOAD BACKGROUND
- what is it? (Hal)
- shuffling (Hal)
- lozenges (Rachel)
- ALTERNATING SIGN MATRICES
- definition (Geir)
- relation to TOADs (Kristin)
- as DPFLs (Geir)
- CONJECTURES
- Baxter Permutations (Dominic and Nick)
- ASM shuffling conjecture (Boytcho)
- A(n-1) conjecture (also known as the proper linking conjecture)
- INTERESTS
- lozenge tiling flux lines (Rachel)
- probability of certain ASMs (Pavle)
- DPFL linking probabilities (Kristin)
Materials
- COMPUTER
- Jim will bring his laptop
- Hal will send a tarball with programs
- T-SHIRTS
When preparing a paragraph, picture, or presentation of the assigned
topics, people should scan in necessary images, send the images to
Boytcho, and send images and text to Rachel who will compile
everything. Boytcho will make all of the images look nice with xfig.
Volunteers to attend the URS, and the times they are available:
- Hal: 9:00-10:00, 12:30-end.
- Kristin: 12:00-2:00
- Joel: 9:00-1:00
- Dan: 2:30-5:00
- Nick: 2:30-5:00
To show the relationship between Aztec Diamonds and ASMs at the URS,
we do not have to explain height function or the algorithm used to
find the ASMs from these heights. Instead, we can use a simpler
method:
Look at the vertices in an Aztec Diamond that correspond to
the entries of the larger (size n+1) ASM. Count the number of edges
that meet at each vertex. This number will be a 2, 3, or 4. Subtract
3 from the number (this will yield a -1, 0, or 1). This produces an
ASM from any tiling of an Aztec Diamond.
We can use a similar method to find the smaller (size n) ASM. Count
the number of edges that meet at each vertex. This number will be a
2, 3, or 4. Subtract this number from 3 (this will yield a -1, 0, or
1). This produces an ASM from any tiling of an Aztec Diamond.
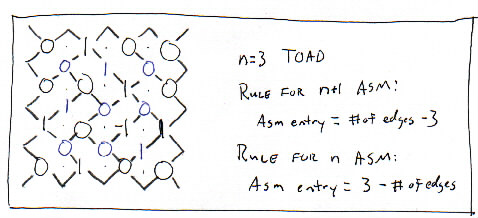
Mathematics
A Question (perhaps for Pavle): can we prove or even verify this
conjecture?
Conjecture: If x and y are two different n-by-n ASMs,
then the number of size n+1 ASMs that are compatible with both x and y
is equal to the number of size n-1 ASMs that are compatible with both
x and y.
In other words, if x and y are two different nodes on the same level
of the ASM tree diagram, is the number of way to connect them by going
up one level and back down is equal to the number of way to connect
them by going down one level and back up.
Question: (posed by Joel and Geir) How many ASMs are there with
only one -1? with two -1s? More?
Partial Answer: If there are A(n) ASMs of size n, there are A(n) - n!
ASMs with one or more -1's in them. There are (n choose
3)2*(n-3)! ASMs with one -1.
Question: How many ways are there to go up k levels, starting
from the bottom? (1,2,8,80,...) Maybe there's a nice theorem lurking
there.
Jim's article titled "The Many Faces of Alternating Sign Matrices" is
due by April 20th. So everybody should prove important stuff by
then.
Rachel asks: What does p-adic continuity mean?
That leads to a Conjecture: The number of domino tilings of an
n-by-2n rectangle is
always odd. (Can we prove this by showing that for any n, we can
match Dominos into pairs with a remaining singleton?)
Abe asks about Components and Linkages. He wants to know a
good way to count the number of components of a matching. Jim gives a
good answer: First, see what even number 1 matches with.
Next, move one place to the right. See what even number this number
matches with. Again, move one place to the right. See what even
number this number matches with. etc.
Baxter Permutations
Dominic: What's the deal with the two different definitions of Baxter
Permutations? For example, one definition works only on odd numbers.
Another definition works on any number. How do these two definitions
relate?
Note: Hal will introduce some notation into the notes.
I hope this helps.
The object of interest here is an order n Aztec Diamond where both of
the corresponding ASMs are permutation matrices. (An ASM without -1's
is a permutation.)
If we take a size n+1 permutation matrix, there is exactly one size n
compatible ASM, because we know that the number of of smaller
compatible ASMs are 2^(# of -1s in the bigger ASM) = 2^0 = 1.
This smaller ASM may or may not be a permutation matrix. If it
is a permutation, then we conjecture that the size n+1 ASM is a
type II Baxter permutation.
What is the difference between a Type I Baxter Permutation and a Type
II Baxter Permutation? A type I permutation is odd in size (2n+1),
and sends odds to odds and evens to evens. If we take out the odd
elements of the type I Baxter Permutation (1BP) we get a size n+1 Type
II Baxter Permutation (2BP). We think that each 2BP corresponds with
exactly one size n permutation that, when put together, form a 1BP.
According to the Baxter Permutation Conjecture, each size n+1 2BP is
identical to a size n+1 ASM without -1's whose single compatible size
n ASM is also has no -1's. Furthermore, if we construct a permutation
matrix Pi,j of size 2n+1 where if i and j are odd, they
correspond to entries of the size n+1 ASM and if i and j are both
even, they correspond to entries of the size n ASM, and if i and j are
not both odd or even, the entry is zero; then P is a 1BP corresponding
to the original 2BP.
Example 1
+ 0 0 0 + 0 0
0 + 0 and + 0 0 0 are compatible.
0 0 + 0 0 + 0
0 0 0 +
As permutations:
2 4 6 and 3 1 5 7
We can rewrite that by interspersing the ASMs:
0 + 0 0 0 0 + 0 0 0 0
+ 0 0 0 + 0 0 0 0 0
+ 0 0 0 + 0 0 0 0 0 0
0 + 0 --> 0 0 0 + 0 0 0 --> 3 2 1 4 5 6 7
0 0 + 0 0 0 0 0 + 0 0
0 0 + 0 0 0 0 0 + 0
0 0 0 + 0 0 0 0 0 0 +
For example: 3 1 5 7 (1 maps to 3, 3 maps to 1, 5 and 7 map to
themselves) induces 2 4 6 (each maps to itself). Thus we have 3157
and 246. But we can write these two permutations as one larger
permutation as follows: 3214567.
Question: How does a size n+1 2BP ``induce'' a size n
permutation?
Example 2
0 0 + 0 0 0 +
0 + 0 and 0 0 + 0 are compatible.
+ 0 0 + 0 0 0
0 + 0 0
As permutations, we can write them as 3 2 1 and 3 4 2 1.
We claim that 3 4 2 1 is a 2BP.
We can construct a 1BP from these two permutations:
3 2 1, 3 4 2 1 --> 6 4 2, 5 7 3 1 --> 5 6 7 4 3 2 1
Conclusion:
We seem to have missed the big clue that was set out in front of us:
the existence of two types of Baxter Permutations, along with the fact
that a TOAD corresponds to two ASMs.
SSL Minutes
29 March 2001
Dominic Johann-Berkel
Baxter Permutations:
Dom presented information about Baxter Permutations:
In 1954, Eldon Dyer asked the following question: Let f and g be
continuous functions that commute under composition (that is, f(g(x))
= g(f(x)) for all x). Let f and g map the unit interval [0,1] into
itself. Must f and g have a common fixed point, meaning a point z
such that f(z) = z = g(z)?
Though William Boyce ultimately proved this false, the investigation
of Dyer's conjecture yielded interesting information. Specifically,
if f and g do have a fixed point (in fact, if they have finitely many
fixed points), then the pair of commuting functions induces a Baxter
permutation.
If N denotes an odd natural number, IN denotes the set of natural
numbers through N, ON the odd elements of IN, EN the even elements of
IN, and P is the permutation P: IN --> IN, then we can define a Baxter
permutation as follows:
Def: P: IN --> IN is a Baxter permutation (Type I) of order N if and only if
1.) P(ON) = ON, P(EN) = EN;
2.) If P(n) is between P(2i) and P(2i + 1), then n = 2i;
3.) If P(n) is between P(2i - 1) and P(2i), then n = 2i.
(Note: This is the definition of what we have been calling a Type I
Baxter permutation. At this point in my presentation, I should have
defined a Type II Baxter permutation since the rest of my talk was
primarily concerned with Type II Baxter permutations.)
Following the definition, I argued (admittedly, rather weakly) that
there was a correspondence between Baxter permutations and thee
non-intersecting paths. This correspondence consists of composing two
bijections. The first one joins Baxter permutations and twin binary
trees, the second one joins twin binary trees and three
non-intersecting paths.
For the sake of simplicity, I will reconstruct my argument through a
different (better) example. In class, I applied my argument to the
following Type I Baxter permutation: 3 2 1 4 5 6 7. The paper which
outlines the argument uses Type II Baxter permutations. Thus, I will
proceed by examining a Type II Baxter permutation.
Def: A permutation P of Sn is a Baxter permutation (Type II) if and
only if, for all integer m?[n - 1], P can be uniquely factorized by:
P = P'.m.P<. P>.m+1.P'' or P = P'.m+1.P>.P<..m.P'' Where
all the numbers of P< (respectively P>) are less than m (respectively
greater than m + 1).
Thus, according to this definition, 4 2 3 6 5 7 1 is a Type II Baxter
permutation of order 7. For example, for m = 4 we have P< = 2 3 and
P> = 6. For m = 1, we have P> = 3 6 5 7 and P< = X. Etc.
Lemma: There is a bijection between Baxter permutations (Type II) on
[n] = {1,2,,n} and twin binary trees. Proof: For simplicity's sake,
I omit the proof. To see a copy of the proof, please see (S. Dulucq,
O. Guibert, Mots de piles, tableaux standards et permutations de
Baxter, 6th Formal Power Series and Albegraic Combinatorics Conf.,
Dimacs, 1994, Discrete Math., to appear).
Ex: Look at the Type II Baxter Permutation 4 2 3 6 5 7 1.
According to the Lemma, there is a bijection between this permutation
and a pair of binary trees. We show this bijection through an example:
4 2 3 6 5 7 1
1 7
/ \ / \
2 6 1
/ \ / \ |\
4 3 4 5
/ \ / \ \ |\
5 3
/ \ / \
6 7 2
/ \ / \ / \
To form the first tree (the increasing tree), we start with the least
value in the permutation, 1. Then we see where the next value, 2, is
in relation to the one. It is to the left, so we draw a stem downward
to the left. Next, we see where 3 is in relation to 2. It is to the
right of 2 and still left of 1, so we draw a stem downward and to the
right from 2. Next, where is 4? It is to the left of 3, but it is
also to the left of 2. Thus, we will draw a stem downward and to the
left from 2. 5 is to the right of 3. 6 is to the left of 5. And 7
is to the right of 5. Since each number in the binary tree must have
two descending branches, one to the left and one to the right, we can
add "leaves" to the binary trees as shown by the dotted lines. Thus,
every number has either two descending stems, one descending stem and
one descending leaf, or two descending leafs. To form the other,
decreasing, binary tree, we start with the greatest value in the
permutation, 7. We repeat the same process until we form another
tree. The increasing and decreasing binary trees form a pair of twin
binary trees.
Lemma: There is a bijection between binary trees and pairs of
non-intersecting paths (there are more details, but for the sake of
this discussion, this much will suffice).
Proof: Again, for simplicity's sake, I will omit the proof. See
(S. Dulucq, O. Guibert, Baxter Permutations, 1998, Discrete Math.,
180, 149).
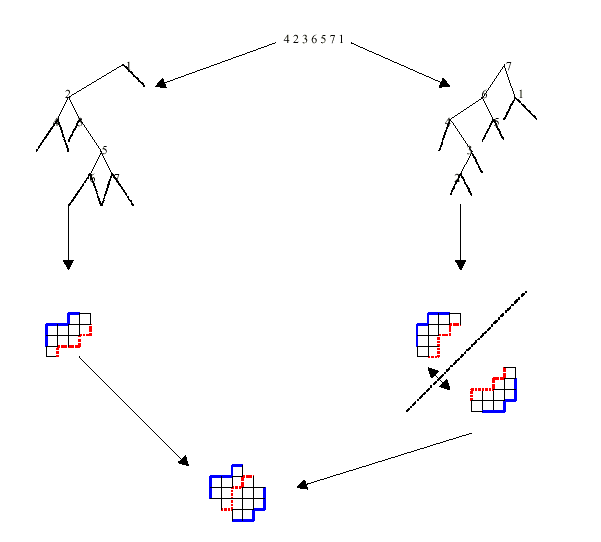
This correspondence is equivalent to travel in prefix order the
completed binary trees and to code, respectively, the internal edges
and the leaves. The first paths (shown in blue) are obtained by
coding the internal left (respectively right) edges by a North
(respectively East) step. The second paths (shown in red) are
obtained by coding the left (respectively right) leaves (except the
two extreme ones) by an East (respectively North) step.
Thm.: There is a bijection between twin binary trees and three
non-intersecting paths.
Proof: According to our previous lemma, twin binary trees correspond
to a pair of two non-intersecting

That about does it. That is what I attempted to demonstrate during
Thursday's meeting. In hindsight, I would have done quite a few
things differently, but I hope the preceding explanation helps clear
things up. For information related to Baxter permutations, or to see
more rigorous demonstrations of what I tried to talk about, please see
any of the following articles:
W.M. Boyce, Generation of a class of permutations associated with
commuting functions, Math Algorithms 2 (1967), 19-26.
S. Dulucq, O. Guibert, Mots de piles, tableaux standards et
permutations de Baxter, 6th Formal Power Series and Albegraic
Combinatorics Conf., Dimacs, 1994, Discrete Math., to appear
S. Dulucq, O. Guibert, Baxter Permutations, 1998, Discrete Math., 180,
143-156.
F.R.K. Chung, R.L. Graham, V.E. Hoggatt, M. Kleiman, The number of
Baxter permutations, J. Combin. Theory Ser. A 43 (1986) 1-22.
I have more articles if you're interested, but these are the most
interesting ones.
SSL Minutes
5 April 2001
Nick Pongratz
Debriefing of Undergraduate Research Symposium:
- Overall spectator attendence seemed a bit low.
- During the debriefing, Nick learned a thing or two about the
grammatical use of "good" vs. "well"
- Tips for next time:
- Make the posters more visual (more cool images, less
"boring" text)
- Don't wait till last minute.
We then went around the room for ~4 minutes each:
Abe: Was thinking about the A(n-1) conjecture.
How to solve? - Find a bijection.
- Boytcho: fill in edges of blue-red DPFL, flip coin to
determine where to place horizontal lines, vertical
lines are then forced.
Dominic: Will send out to the list the algorithm to generate Baxter
permatations of any order n. (specifically, Hal, Boytcho, Nick wanted
it.)
Would like ideas on how we'll prove Baxter conjecture.
Nick: Working on a program that determines if a given
permutation is a Baxter permutation. After that, will start coding
the Baxter permutation generator.
Kristin: "Where is everyone?"
Asked Abe if he has a program to count linkings of DPFLS's. Abe said
the program is almost done.
Dan: Would like to get involved with a project with Hal and Rachel.
(Which project is this?)
Boytcho: Has been looking to unify the two definitions of
Baxter permutations.
Jim says we should think about height functions when thinking about
proving the shuffling conjecture.
Hal: Wanted to know what the final version of his applet should
do: Boytcho suggested including a way to manually make elementary
moves. Abe suggested it show the height functions. Debate over
implementation ensued. Should we have toggle buttons or separate
versions as we add features? Jim would like a "turbo mode with
autopilot" and a tutorial mode. Michael suggested the code be
modularized.
Jim encourages us to set up our own focussed meetings.
Everyone should meet with Michael next week (April 9-13) for 15-45 min. Email
him a time that will work well.
SSL Minutes
10 April 2001
Boytcho Dontchev Peytchev
Misc.
Boytcho may need to be reminded about the bringing of beverages for today.
We need T-shirts to be designed.
Ideas that were expressed:
- pretty pictures with the code that produced them as a background
- the cochineal animal
- as there is a history of T-shirts involving images that relate
in one way or another to what we're doing the picture of the
hexagonal DPFL was brought up as a novelty.
In order to talk about things we need a nice way to name them. Among
other reasons there's also the reason of having things published.
Worked on the Proper vs. Rigid linkings. Geir suggested that we call
the proper linking "sequential". We can represent each of the pairings
as lattice paths and it was suggested that we call the proper linking
"Short" and the rigid linking "Tall".
The record shows, that prof. Propp will ask John Conway about names
for things.
Then there were round robin, ``What have i been up to?''
Kristin was working with Abe on code that counts specific pairings of
DPFLs
Boytcho was playing with Baxter Permutations
Joel is working on what was referred to as "reduced DPFLs" or maybe
"even DPFLs" which arise when the black vertices are removed from a
chessboard colored graph with a DPFL. One question is how much info is
lost in the transition from the complete to the reduced DPFL.
Dan has managed to avoid paying attention to his classes with the help of
honeycombs.
Jim is trying to extrapolate the number of tilings of a 2xn rectangle
(by dominoes, ribbons, whathaveyou) into the realm of negative n.
Geir is looking at the A(n-1) conjecture with both ASMs and DPFLs
Hal's been hacking the domino shuffling thing.
Nick is working on a BP verifier and wants to get to a generator based
on that.
Dominic is working on a different (?) BP generator.
At this point it was suggested that we may want to look into things
that BARELY FAIL to be BPs and TOADs with very few -1 in the
corresponding pair of ASMs. Is there any correlation in the two?
The question was raised if ppl have difficulties accessing the
literature. If so Prof. Propp and Michael Lang may be able to
facilitate that on a case by case basis as ppl contact him.
It was observed that an Annotated Bibliography would be A Good
Thing. Geir was appointed chief maintainer of said Bibliography.
Then we made a List. The List was of Areas Of Interest in the
group. Neither five, nor seven are of them, yet there are six as
follows:
- the A(n-1) Conjecture:
Geir, Abe
- The Baxter Permutation Conjecture:
Boytcho, Dominic, Nick, Hal, Geir
- Hexagonal DPFLs:
Dan, Boytcho, Rachel, Hal
- "even" DPFLs:
Joel
- Software:
Hal, Boytcho
- Specific pairings:
Kristin, Boytcho, Abe
The subsets of SSL outlined above, should schedule meeting times
between themselves to work on the things they find of common
interest.
In B107, Michael showed us a couple programs which are on dodgson:
vaxrandom and printtiling. These programs can be found in Jim's
directory. vaxrandom is a program which allows you to tile virtually
any region you tell it to, While printtiling will make a pretty
PostScript file out of the plaintext given by vaxrandom
another thing that was mentioned was drawtile.
some net-resources that are of use are:
http://www.ams.org/mathscinet/
http://www.research.att.com/~njas/sequences/index.html
People who find themselves lacking software that would help them get
things done that they want done should contact Michael, who would then
relate people's desires to the Coders among us.
have fun
B.
SSL Minutes
12 April 2001
Geir Helleloid
Pavle has left us for the rest of the semester. Goodbye Pavle.
Question: Given a random ASM, what is the average value in a given matrix
position (where the average is weighted by the number of paths to the ASM
in the shuffling lattice)?
Example of how to run a process in the background:
Create a file - let's name it "runbr" - and make it executable.
(chmod 755 runbr)
In runbr, have one line, e.g,
blue-red 10 > br10
Then start the process with:
nohup runbr &
Question: What happens if you convert TOADs to single ASM's (by
interleaving the entries with zeroes and getting an ASM of order 2n+1)?
Are there any patterns you can find (in the DPFLs, etc.)?
After this question, Hal began his presentation on his proof of the Baxter
Permutation Conjecture.
After Hal spoke, we adjourned to the computer lab, where we did our own stuff.
SSL Minutes
17 April 2001
Nick Pongratz
We had two guests, Dan and Chris.
We went around the room getting caught up on everyone's progress:
Michael- is polishing part of his dissertation.
Abe- has been listening to Hal explain his proof.
is soliciting comments for brhelper.
Jim- 1: working on article, "Many Faces of ASMs," would like to put in a
section, "Pairs of ASMs" if Hal's proof is convincing.
2: another article, "Z^2 Action".
3: has been playing around with hexagonal DPFL's
4: Terminology: DPFL should maybe be called Fully Packed Loops.
Rachel would like to call DPFLs Aztec Phoenix Feathers.
Everyone likes the terms "proximal" and "distal"
Dominic- explained how a counterexample to Hal's proof does not work.
is going at the Baxter Conjecture differently than Hal.
Hal then explained to our guests what we're doing with Baxter Permutations,
ASMs, and TOADs.
Nick- is taking Mike's advice with the Baxter Permutation verifier, will
simply separate each element on the commandline by a space (IOW, let
UNIX and C do the tokenizing).
has worked on that a little bit since the weekend.
Geir- working on A(n-1) conjecture.
typed up unannotated unlinked bibliography.
Kristin- last week played around with computers with Michael.
looking for patterns of different growth rates. Was given the advice
that most UNIX shells offer the command "factor" and Maple has
"ifactor", both of which factor a number into primes.
Dan- had all of his exams on one day. Brutal.
Joel- hasn't done much over the holiday weekend.
Rachel- found there are no "rigid" pairings of hexagonal DPFLs.
Hal- Explained his proof for the Baxter conjecture. Didn't completely finish,
will finish at next meeting.
SSL Minutes
19 April 2001
Dominic Johann-Berkel
Nick will bring the beverage for next Tuesday's meeting.
We discussed what we would like to have on our shirts. Possible ideas:
- Hexagonal FPL
- ASMs with a superimposed Aztec Diamond
- Show everthing (TOAD, ASMs, DPFL, etc.) so people can see how
they are related.
It was decided that Dan and Joel (since they were not present at the
meeting) will be responsible for organizing, choosing, and producing the
shirts. Ha. Seriously, if anybody has an idea for a shirt design, make a
mock up design to present at Tuesday's meeting. Otherwise Jim and Mike
will draft somebody to head the shirt project, or we might scrap the idea
all together.
Hal announced that he will be giving a talk on Monday at 4:30 in room 2321
Sterling Hall (the Physics Club room) regarding undergraduate research.
Coffee and cookies will be served.
Hal continued with his proof of the Baxter Conjecture. He outlined his
proof for the second half of the conjecture. That is, Hal showed that,
when viewed as a permutation matrix, a Baxter permutation in the larger ASM
and the existence of a -1 in the smaller ASM are the same thing.
Dominic then presented a different method of approaching the Baxter
Conjecture. While Hal's method works from the outside inward, Dominic used
a method that worked from the inside outward. That is, he used Hal's
method to determine all the zeros of the smaller ASM. Then he looked at
all the remaining "undetermined elements." There are three cases:
- The undetermined element is flanked by two 0's and two 1's.
0 1
x
1 0
In this case, the undetermined element must be a 1. If it were anything
other than a 1, there would be no possible way to tile the area with
dominos; there must be a 1-by-1 square somewhere.
- The undetermined element is flanked by three 0's and one 1.
0 1
x
0 0
In this case, the undetermined element must be a 1. If it were a -1, then
there would be no possible way to tile the area with dominos; there must be
a 1-by1 square somewhere. The undetermined element cannot be a 0. To see
this, we must examine three cases. In each case, a shape is forced to
propagate to the edge of the Aztec Diamond. But this shape does not fit
the edge shape of an Aztec Diamond. Thus, we have a contradiction, and the
undetermined element cannot be 0.
- The undetermined element is flanked by four 0's.
0 0
x
0 0
In this case, the undetermined element cannot be a 0. To see this, we
assume it is a 0 and derive a contradiction. We must examine four cases.
In each case, we propagate a shape through the larger ASM until we hit a 1.
Then the shape changes to a shape that continues propagating to the edge
of the Aztec Diamond. But this shape does not match the edge of an Aztec
Diamond. This is a contradiction, so the undetermined element cannot be a 0.
Thus, we can always determine all the 0's of a smaller ASM. We can then
alternate between 1 and -1 for the undetermined elements in a given row or
column, and proceed with the proof as Hal described.
Next, we went around the room to see what people had accomplished since
Tuesday's meeting.
Abe: nothing
Dom: the above method of proving Baxter
Nick: nonBaxter stuff
Geir: not done much since Tuesday
Kristin: not done much since Tuesday
B'cho: not done much since Tuesday
Hal: Baxter stuff
We then retired to the computer lab where we each worked on our own stuff.
SSL Minutes (Part 2)
19 April 2001
Nick Pongratz
Here's the few notes I took dealing with the programming of reusable components
for further research:
We want an ASM class.
Variables: storage array (char)
size of ASM
Constructors:
fromMonotone
fromHF
fromPermutation
fromFPL
Methods: find_bigger_compatible( *function(ASM))
find_smaller_ " " "
display
elementary moves
That's all I have. I know we talked about more stuff, but my notes kind of
drift off. What else do we need? What do we have implemented, Boytcho?
SSL Minutes
24 April 2001
Rachel and Geir
Geir and Rachel took notes.
We had another visitor, a post-doc, called Rebecca. She is a possible
candidate for leading SSL next year in Jim's absence.
We talked about tee-shirt ideas. No one had designed a concept over the
weekend and with the end of the semester coming we are getting
desperate! Rachel, Kristin and Dominic were willing to make the final
decision of what to put on the shirt and get it all together to be sent
out. Geir and Hal said they would put together their own concepts to give
to us for Thursday's meeting. Mike suggested we use an idea from the
Baxter conjecture and proof since that seems to be the only major new
things completed this semester. Other ideas generated from the group are
random tiling an actual toad! to combining matrices and tilings in layers
on the shirt (although the tilings have been on previous shirts, so it
wouldn't necessarily show new things accomplished this semester). One
thing or another, we need to get cracking on this, and choose a concept for
the shirt by the end of this week!
Things to work on in research: PARTIAL RESULTS should be written down and
sent to the rest of the group. This is beneficial to everyone in the
group! For example, it helps to prevent repetition and making the same
mistakes as someone else in the group who already did. Please send out
partial results!
Additionally, send out QUESTIONS that you want to be answered that you
cannot answer yourself. Nick volunteered to keep the question list, so
please send your questions to Nick.
Mike sez:
Please don't restrict yourself to questions you can't answer yourself.
I think it would be nice if this list had all the questions you can think
of to ask, whether you've tried to answer them or not. If you have, then
include whatever progress you've made. I'll send out another example in
the next message.
There are some modifications mentioned to Hal's applet. Dan volunteered to
help. An example of these would be to outline the open squares that come
in the shuffling of the applet so that the viewer will more easily see
what's going on.
Mike sez:
Another mod would add arrows to the tiles to show which direction they will
move.
There was a question related to the An-1 conjecture about connections from
the first terminal to the 2n terminal and "reeling in" the linking. I had
forgotten I was taking notes and forgot to write down what the actual
question was. (Mike?) No one volunteered to work on this one.
NOTE: next WEDNESDAY MAY 2nd our group is speaking to VIGRE at noon! Think
about what you can do to participate in this, if you want to discuss your
research, etc.
Progress reports:
Dominic is studying on path connections on an ASM leading to an
undetermined element.
Nick is programming, looking at non-Baxter stuff.
Dan ?
Geir is working on the An-1 conjecture.
"Baxter boy" (Hal) is putting his proof on paper.
Kristin is comparing data on FPLs.
Boytcho has been sick, has not been able to do much.
Rachel is putting together her hexagonal proofs, will write them up to send
to the group.
SSL Minutes
26 April 2001
Hal
Jim Asks what Pavle passed on to people. Should we check the notes?
Jim asked about the up-down conjecture. We told him that the next big
programming push will be to check that out.
Kristin should email out her results (linking probability numbers)
soon (DONE).
Question: What are the average number of components of the
DPFL/FLP/EIEIO matchings? Abe will look at that.
That led to another question: What is the proper way of counting
components? There are two natural answers:
- Break the DPFL/FLP between 2n and 1.
- Take the max number of components that can be produced by
breaking the DPFL/FLP at any place.
How was it done in that theorem for lattice paths?
We heard a story about where the gyrational symmetry came from.
The theorem was first stated as something that was obviously not
true all the time, but then it turned out that it was. The moral of
our story has something to do with our intuition.
I forced Rachel to take a stand on whether she believes in
gyrational symmetry for Hexagons. She says no, but was unwilling to
place money on it.
Rachel then talked about her theorem about the lack of what would be
a distal matching of an ASM-DPFL in hex-DPFLs. The thing that Jim
called a hole in her proof has been proved, but Rachel did not
explain how she filled it very well. But I understood.
We talked about the stupid t-shirts.
The Last Supper will be on the 17th at 6pm. We will
not be eating at Domino's Pizza. Somebody noted that we have
the right number of people for the last supper (12+1).
The VIGRE Lunch
Wednesday the 2nd at 12:00pm.
I am still confused about this. Do I have to prepare anything for
this?
The whole week after this (6-12th), Jim will be in the Black Forrest.
Back to the lunch: Topics will include the Baxter theorem and
HexDpfl's. Jim will talk, then he'll open things up for general
discussion.
I ask about local moves. Jim says a good way to check would be with
the 7 proximal DPFLs of a given size.
Abe can get to work on programming now that he's finished the paper he
had to write.
Nick wants a web account. I got out my magic wand and gave him one.
Dominic wants to work on the big size 2n+1 ASM that comes from
smushing two compatible ASMs together.
Rachel asks a question. It turns out she was asking about fault free
rectangle tilings.
The Razamov-Stroganov Game
Here is the game: First, pick an N. Then pick a size N square DPFL:
we'll call this one the target. There are two players.
- Player A randomly chooses a DPFL. He wins if his DPFL
has the same matching as the target.
- Player B randomly chooses a DPFL. She then makes exactly
one random mutation to the matching from her DPFL. If the
resulting matching is identical to the target's matching, she
wins.
Definition of Mutation: pick two adjacent terminals i and
(i+1)mod(2n). suppose i connects to j and (i+1)mod(2n) connects to
k.
Reconnect i to (i+1)mod(2n), and j to k. It is possible that i might
equal k to begin with, in which case this mutation changes nothing.
Conjecture: Players A and B have the SAME chance of winning!
Proof for N=3.
There are 5 matchings for this size: two are proximal (P1 and P2), and
three are distal (D1, D2, and D3)
Table of probabilities:
P(A) P1 P2 D1 D2 D2 P(B)
-----------------------
2/7 P1 | 3/6 0/6 1/6 1/6 1/6 | 2/7
2/7 P2 | 0/6 3/6 1/6 1/6 1/6 | 2/7
1/7 D1 | 2/6 2/6 2/6 0/6 0/6 | 1/7
1/7 D2 | 2/6 2/6 0/6 2/6 0/6 | 1/7
1/7 D3 | 2/6 2/6 0/6 0/6 2/6 | 1/7
Look at this as a matrix equation:
2/7 3/6 0/6 1/6 1/6 1/6 2/7
2/7 0/6 3/6 1/6 1/6 1/6 2/7
1/7 = 2/6 2/6 2/6 0/6 0/6 * 1/7
1/7 2/6 2/6 0/6 2/6 0/6 1/7
1/7 2/6 2/6 0/6 0/6 2/6 1/7
This relates to the all-pervasive eigenvalue problem.
Homework: Do this for n=4.
From propp@math.wisc.edu Tue May 1 13:45:00 2001
Date: Tue, 1 May 2001 13:28:38 -0500 (CDT)
From: propp@math.wisc.edu
To: hwcanary@students.wisc.edu
Subject: homework assignment
I think you asked for this:
Read Razumov and Stroganov's new article! And then see if you believe
my new
Conjecture: the relations given by their Conjecture 1, in combination
with the fact that each distal linking-pattern arises from exactly 1
ASM, and in combination with the symmetry property proved by Wieland,
suffice to determine the number of ASMs that give rise to each linking
pattern, and in particular, the total number of ASMs.
Proof for n=3. There are only two geometries that a linking-pattern
can have in this case: proximal and distal. Let P (resp. D) be the
number of ASMs corresponding to any given proximal (resp. distal)
linking-pattern. Pretend for the moment that we don't know P and D.
Since there are 2 proximal and 3 distal linking-patterns, the total
number of ASMs is N = 2P+3D. If the fixed link-pattern that the
players are aiming for is the distal pattern 1<-->6, 2<-->5, 3<-->4,
then player A has a chance of winning equal to
(*) D/N
Now let's compute player B's chances. For each of the five linking
patterns that he could have started with, I give the probability
that he could end up with 1<-->6, 3<-->4, 5<-->2:
1<-->2, 3<-->4, 5<-->6 (proximal): 1/6
1<-->2, 3<-->6, 5<-->4 (distal): 0/6
1<-->4, 3<-->2, 5<-->6 (distal): 0/6
1<-->6, 3<-->2, 5<-->4 (proximal): 1/6
1<-->6, 3<-->4, 5<-->2 (distal): 2/6
So B's chance of winning is
(P/N)(1/6)+(D/N)(0/6)+(D/N)(0/6)+(P/N)(1/6)+(D/N)(2/6)
or
(**) (P/3+D/3)/N
Comparing (**) with (*), we see that the RS conjecture implies
P/3 + D/3 = D
which reduces to
P = 2D.
But now we pull out the fact that each distal linking-pattern arises
from exactly 1 ASM. This gives us D=1, and the formula P = 2D now
gives us P = 2, so we've calculated everything we want to know, and
the number of ASMs of order 3 is N = 2P+3D = (2)(2)+(3)(1) = 7.
Homework (everybody!): For Tuesday, determine whether my conjecture is
true for n=4.
Keep in mind that Ben Wieland has a different conjecture, which relates
A_n(pi) to A_{n+1}(pi') where pi is a linking-pattern of order n and
pi' is a linking pattern of order n+1. Even if the Razumov-Stroganov
relations don't suffice to force the values of all the A_n(pi)'s, maybe
they do when taken together with the Wieland relations (or other relations
that you guys are about to discover!).
And if we can find enough relations to force the values of all the
A_n(pi)'s, then we're halfway towards discovering (among other lovely
things) a new proof of the original ASM conjecture, totally different
from both Doron Zeilberger's proof and Greg Kuperberg's proof!
Jim
We retired to B107, and I made a pretty hexDpfl picture for the
stupid t-shirt. Don't know what others did. Then Rachel, Boytcho, and I went
and had ice cream and beer.
SSL Minutes
1 May 2001
Kristin Jehring
Geir will bring beverages for Thursday, 05/03.
We got off track for about the first 15 minutes, then we went outside.
We briefly discussed the homework. Those who did it saw that Jim's
conjecture holds for order 4. Jim hopes that the Razumov/Stroganov
conjectures lead to a general formula which will give the total number of
ASMs for a specific pairing.
We will have SSL meetings May 15 and 17. The final dinner on the 17th will
close up this semester's SSL. The dinner is set to be at the Wilson Street
Grill, unless someone objects. We agreed to go half with Jim on our dinner.
After the final meeting, you can still meet with Jim or email him. However,
he is moving at the end of May.
Putting stuff on the SSL webpage: email your final, stable documents to Jim
so it can be put permanently onto the webpage.
We need more open questions, so we brainstormed on this for awhile. For
Nick to put on page:
- A(n-1) conjecture
- ASM shuffling conjecture
- How many different ASMs correspond to a given pairing of a DPFL?
Jim mentioned a bunch of questions he wants us to think about and try to
answer in these last two weeks. Some of these were answered as they were
brought up.
- How many different paths connect 1-->2 in a DPEL? Related question,
can you get any length?
- What is the longest path that connects 1-->2?
- What is the average number of loops in a DPFL? What are the lengths
and shapes of the loops?
- If n is odd, can have path that connects the midpoint of two opposite
sides in a DPFL. How many ASMs correspond to this specific pairing?
(Jim had a thought about Catalan objects: Know the average number of
components is 3 at the limit. Look for stats of Catalan objects which might
lead to interesting characteristics of ASMs)
- Can a permutation matrix be reconstructed from its pairing? ANS: NO!
- Given a permutation matrix of order n, how many ASMs of n+1 are
compatible with it?
- In the ASM-compatibility tree, are there as many ways to go up&down as
there are ways to go down&up?
- What is the 'refined' A(n-1) conjecture? [what happens to the 1]
- For lozenge tilings of hexagons, try looking at non-regular hexagons of
the form (a,b,c). Try setting a,b constant.
- If you are counting things, look at the numbers modulo some smaller
number. Try to find 2-adic properties.
- Decorating Dominoes: Connect the six vertices of a domino in some way
and tile a region with these decorated dominoes, try to create paths across
the dominoes.
- Do you see patterns in the patterns?
Jim urges us to expand our minds. Try and come up with new business
methods. Create a new way of looking at a problem or come up with another
problem from one you are working on. Can't solve a problem, try a simpler
one.
Jim got a phone call.
Progress Reports:
Hal worked on writing up his proof. has sent his paper to the
list. Would like to have feedback. Also got his haircut.
Nick & Abe worked on program that would create the
ASM-compatability tree.
Rachel didn't do much over the weekend. Has T-shirt design
made, just needs to compile. Also, need to send the design to the
list to get feedback. Will call t-shirt places to find out costs and
such things.
Dominic looking at the 2n+1 ASM of TOAD. Interested in the
reflections and rotations of the non-Baxter permutation matrices.
Boytcho worked on HW a little, need to digitize the T-shirt design.
Kristin worked on HW, emailed data, got more data, stuck on
proving her conjecture.
Geir read Hal's paper and the Razumov and Stroganov paper.
Dan worked on Hal's applet, added the features Jim asked for,
program has a few bugs now though.
Jim played with nests in DPFLs
SSL Minutes
3 May 2001
Hal
Boytcho mentions that he's extended Rachel's theorem concerning lack
of 2-distal hex-FPLs to semi-regular hexagons.
Jim says that he now officially believes my proof of the Baxter
permutation theorem. I asked him why now and not several weeks ago,
especially since he hasn't yet read my paper. So everyone is
rewarded with exactly one hour of pay. Of course, I'm already up
against the 20hour/week limit.
Charlie the post-doc logician is visiting.
That brought up the subject of how logic relates to tilings. Jim
started talking about a theorem: There is no algorithm that will say
if an arbitrary set of simply connected polyominos can tile the
infinite plane. More precisely, there is an algorithm that can show
that a set of polynomials can't tile the infinite plane, but it may
take an arbitrary length of time to find a counterexample. So the
theorem is co-CE.
Non-trivial theorem: If, for each N, you can tile the NxN square,
allowing for overlaps over the boundary, then you can tile the
infinite region. This gives the co-CE algorithm. (Proof to follow
later.)
Rachel has been bad about filling in timesheets. She also has been
cautious about not including hours spent thinking without writing.
I mentioned that I am not a good accountant, even though I come from a
long line of accountants. Then Rachel said something about coming from
a long line of women. Then we discussed genetics for a while.
Something about X and Y chromosomes and mitochondrial DNA. I really
forget where that discussion was going.
Hal is taking notes.
Going around the room
Rachel is not as sure of her proof about 3-distal hex-pairings
as much as she was a few days ago, but she's working on it.
The t-shirt has yet to be compiled.
Boytcho has what might be a proof of how 2-distal hex pairings
can not exist.
But first, something for the glossary:
Definitions
- ASM FPL - square fully packed loop-state generated from
an ASM. See notes from
20 Feb 2001 for
complicated definition. Easy definition: color the terminals
blue and red, alternating around the edges. start drawing the
inside from left to right, up to down. if there is a zero in
the ASM, make the line bend, and otherwise, make the lines go
straight.
- Hex FPL - hexagonal fully packed loop-state generated
directly from a matching on a hexagon lattice. Simply color
in those edges which are not involved in a lattice.
- proximal pairing - pairing of terminals on an ASM FPL or
a hex FPL such that 1-2, 3-4, 5-6, etc OR 2-3, 4-5, 6-7, etc.
- proper proximal pairing - pairing of terminals on an ASM
FPL or a hex FPL such that 1-2, 3-4, 5-6, etc
- distal pairing - pairing of terminals on an ASM FPL such that
one terminal (call it a) goes to the farthest possible
terminal (call it b), and a-i pairs to
b+i for all i
- 2-distal pairing - pairing of terminals on an Hex FPL that
is equivalent to the definition of distal on an ASM FPL. Has
been shown not to exist.
- 3-distal pairing - The pairing of terminals on an Hex FPL
that contains three equal sized "cables."
|
Boytcho's proof about lack of 2-distal patterns in semi-regular
hexagons starts by assuming there is a 2-distal pattern and picking
the pair that are next to each other. then following the lines around
the edge. One will find that somewhere before getting to the opposite
side, you are forced to pair two adjacent terminals.
But Jim pointed out that he had made a "best-case" assumption during
the proof. then he offered an example of how such a move could turn
bad. He had a bad proof that you can't pick a subsequence of
{1,2,3,...20} where no two elements differ by 3 or 5. The naive
thought is that the best case is {1,2,3,9,10,11,17,18,19}. But the
real answer is {1,3,5,7,9,11,13,15,17,19}.
Jim has been wondering about the FPL/DPFL terminology question.
He needs to get that straight for his talk in Paris.
Mike has successfully defended his dissertation.
He also has looked at other eigenvalues of the Razamov-Stroganov
matrix. He has seen inklings of interesting patters that he doesn't
understand yet.
On another note, Rachel will be in charge of the t-shirt over the
summer, because Jim will not be around.
I give a talk about the history of Hamiltonians. I'll skip that
information right now, except to say that a Hamiltonian can describe a
mechanical system, where the matrix elements correspond to some
potential energy.
Abe bitched about C++. Somebody mentioned that somebody said
that C++ was a practical joke played on programmers. Abe has also
been playing with CVS. He expects the up-down checking program to be
done over the summer.
Dominic is switching schools. He's looking at interspersed
ASMs; maybe he's finding things. Dominic asked Jim about the other way
to form pairings from a TOAD.
.
If you look at the lines we get versus height functions, you see that
we get a contour map. The contour shown represents the contour of
height 3.5. There Polynomially many pairings for some reason. We
noticed interesting things that go on in the frozen regions.
Nick has been playing with Baxter permutations and helping Abe
with the Compatibility Graph Program.
Somebody mentions that there are a lot of mathematicians in France.
Geir forgot to bring the drinks he bought.
Dan asks about the compatibility graph. Then he asks about
compactness and tilings.
Jim gave a beautiful diagonalization proof of that non-trivial
theorem he mentioned before.
Kristin asks about how the Razamov-Stroganov implies something.
Then we talked about the eigenvalue problem.
Then we all went and had a picnic under Van Vleck's tower. That was
successful.
SSL Minutes
15 May 2001
Hal
No one volunteered to bring drinks on Thursday.
Somebody asked about gyration on a Hex FPL.
Somebody asked Dominic what progress he has made on the Doubled-ASM
FPL (The ``naturally interleaved'' kind). No numbers as yet.
Definition: A pairing is rigid if it has only one
corresponding hex-tiling or ASM.
Definition: a pairing is locally rigid if there are no
local moves that can be made which preserve the paring but change the
tiling/ASM.
If there was a complete set of local moves for a given system,
then the two definitions for rigidity would be equivalent.
That reminds me: I was going to look into the question of local
moves.
Fun Summer Projects
Ribbon Tilings
Let me refer you to Chris Moore's email to the domino group.
Date: Wed, 9 May 2001 14:09:40 -0600 (MDT)
From: Cris Moore <moore@santafe.edu>
To: domino nos@pam math.wisc.edu
Subject: ribbon tiles
Fellow domino'ers, you may enjoy finding bijective proofs of the following
two things, which I'm thinking of writing a little note about when I get
the time. Recall that a ribbon n-omino (or n-ribbon for short) is a path
of n squares connected by stepping North or East (note rotations are not
allowed). There are 2^(n-1) distinct n-ribbons.
Let N(x,y,n) be the number of tilings of x by y rectangles with n-ribbons.
Then
1) for all n > x, N(x,kn,n) is a function only of x and k. For instance,
there are exactly as many ways to tile a 3x8 rectangle with 4-ribbons as
there are to tile a 3x10 rectangle with 5-ribbons.
2) for all n, N(n,n,n) = n!
Both of these have easy proofs which I'm sure you'll have no trouble
finding... just remove diagonals of squares running NW-SE that each ribbon
crosses exactly once, converting n-ribbons to (n-1)-ribbons.
- Cris Moore
Jim showed us the easy proof of item (2), then asked us to
come up with some other questions. Here they are:
-
How many ways to tile a 2n by 2n rectangle with n-ribbons? I came up
with a lower bound of (2n)! and thought for a while that that might be
an exact answer. But then Jim came up with (n!)^4 as a new lower
bound.
-
How many ways to tile a 2n by n rectangle with n-ribbons?
-
How many ways to tile a l by m rectangle with
n-ribbons?
-
How many ways to tile a n+1 by n rectangle with n-ribbons?
We then talked about local moves on a ribbon tiling. I forget who
invented these. Take two ribbons that lie next to each other for a
while and swap their tails. They'll still be the same length, and
take up the same space, but be in a different configuration.
Rectangular FPLs
What about square FPLs on a n-by-m grid? You would have to play with
the boundary conditions for an odd-by-even grid. Jim said he had
dealt with this in part 5 of "The many faces of ASMs". I think that
he called them partial ASMs.
I then had an epiphany about hex FPLs. See my write-up.
Progress Reports
Nick worked on a project for one of his classes.
Boytcho is writing up some stuff.
Abe studdied up for his exams. This week he'll do the
glossary, and over the summer he'll learn about gyration.
Dominic has been obsessing about the sequence 16, 17, 20, 22,
24, 31, 40, 121. He's also been looking at the ``naturally
interleaved'' ASMs, as mentioned before. He wants to modify TOAD
Shuffler to show the funny lines mentioned in the notes from two weeks ago.
I have been busy with my paper.
Mike glanced at the eigenvalues of the R-S matrix again.
Jim went to a conference. He talked about Penrose tilings and
how to produce one without mistakes by moving a pair of pentagons
around the plane. Without benefit of a chalkboard, I didn't follow
that very well.
Then we called it quits.
SSL Minutes
17 May 2001
Dominic & ...
Baxter Permutations
Hal makes a conjecture that a series of moves such as the one
described below can produce (1) only baxter permutations and (2) all
of the baxter permutations. He was right on (1), but not on (2).
Counterexample for (2): permutation 152436.
Dominic produced the following proof of (1):
Given any identity matrix, we can transpose any any number of 1's along the
diagonal. For example, we can take
100000
010000
001000
000100
000010
000001
and transpose the four interior 1's to get
100000
000010
000100
001000
010000
000001
Claim: any such transposition (and successive transpositions) will yield
a Baxter Permutation.
Proof: Recall that a Baxter Permutation can be defined as any permutation
that fits #.p.p<.p>.p+1.#' where # and #' are unimportant, p is any number
in {1,2,...,n-1}, p< is a sequence of numbers less than p, and p> is a
sequence of numbers greater than p.
Let [ ] denote the list of numbers that we are transposing. In the
previous example, [ ] would contain the numbers 2,3,4,5.
Case 1:
Assume p and p+1 are both outside [ ]. This means both are either less
than or greater than each number in [ ]. Then all of [ ] is in either # or
#'. This is the unimportant stuff. So transposing [ ] does not affect p
or p+1. they are still adjacent to each other in the ASM, so p< and p> are
both empty. This fits the definition of a Baxter Permutation.
Case 2:
Assume p and p+1 are both inside [ ]. Then transposing [ ] will not
separate p and p+1. They will still be adjacent to each other. So again,
p< and p> are empty. This again fits the definition of a Baxter Permutation.
Case 3: Either p or p+1 is inside [ ], but not both. If p is inside [ ]
and p+1 is not, then p must be the maximum element in [ ] (recall we
started with the identity matrix). Then transposing [ ], we get:
[p-k ... p-2 p-1 p] p+1 -----> [p p-1 p-2 ... p-k] p+1.
But this fits the definition of a Baxter permutation with p< containing
p-1...p-k and p> as the empty set. If p is outside [ ] and p+1 is inside,
then p+1 must be the minimum element in [ ]. Then transposing [ ], we get:
p [p+1 p+2 p+3 ... p+k] -----> p [p+k ... p+3 p+2 p+1].
But this fits the definition of a Baxter permutation with p> containing
p+1...p+k and p< as the empty set.
Thus, any transposition of elements along the diagonal of an identity
matrix (and any successive such transposition) will yield a Baxter
Permutation.
That finishes the proof.


 There was a longer discussion over our second problem, using domino
shuffling to prove that H(2,2,2,) = 20. The claim in the paper is, in
order to count perfect matchings of these tiled hexagons, first "flatten"
them into square grids, and then count. Give each matchings weights for
example, for this graph (Figure A) we have cde + aef + bcg. Give weights
of zeroes and ones, with zeroes to the vertical edges so that they don't
contribute to the sum.
There was a longer discussion over our second problem, using domino
shuffling to prove that H(2,2,2,) = 20. The claim in the paper is, in
order to count perfect matchings of these tiled hexagons, first "flatten"
them into square grids, and then count. Give each matchings weights for
example, for this graph (Figure A) we have cde + aef + bcg. Give weights
of zeroes and ones, with zeroes to the vertical edges so that they don't
contribute to the sum.
 Boytcho had a question about how do we fit these flattened hexagons into an
Aztec diamond graph? NOTE: there IS a difference between an Aztec diamond
and an Aztec diamond graph! (my name is gecko, not to be confused with
geico, which can save....) See Figure B as an example to differentiate
between the two.
Boytcho had a question about how do we fit these flattened hexagons into an
Aztec diamond graph? NOTE: there IS a difference between an Aztec diamond
and an Aztec diamond graph! (my name is gecko, not to be confused with
geico, which can save....) See Figure B as an example to differentiate
between the two.



 avle will be the Beverage Person for Tuesday next.
avle will be the Beverage Person for Tuesday next.
 achel said something about brownies.
achel said something about brownies.