A combinatorial interpretation of the
sequence 1, 1, 2, 6, 21, 77, ...

Reid Barton
REACH

October 26, 2002

What is the sequence?

The sequence $\{b_n\}_{n\ge 0}$ is defined by the recurrence relation

$\begin{displaymath}b_0 = b_1 = 1, \quad b_{n+1} b_{n-1} = b_n^2 + b_n\hbox{ for $n \ge 1$ }\end{displaymath}$

and begins 1, 1, 2, 6, 21, 77, 286, 1066, ....

Why is it interesting?

It gives the numbers appearing in the ``number fence'' table

$\begin{displaymath}\begin{array}{cccccc} \cdots&1&1&1&1&\cdots \\ \cdots&1&1&1&... ...\cdots&6&6&6&6&\cdots \\ \cdots&21&21&21&21&\cdots \end{array}\end{displaymath}$

where the top two rows are filled with ones and each number is the determinant of the matrix formed by the four numbers touching it. In other words, the matrix satisfies the recurrence

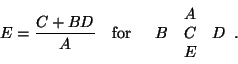
$\begin{displaymath}E = \frac{C + BD}A\quad\hbox{for}\quad \begin{array}{ccc} &A& \\ B&C&D \\ &E& \end{array}. \end{displaymath}$

It turns out that if we apply this recurrence relation to a table whose top two rows are filled with formal indeterminates

$\begin{displaymath}\begin{array}{ccccccc} \cdots&x_{-2}&x_{-1}&x_0&x_1&x_2&\cdots \\ \cdots&y_{-2}&y_{-1}&y_0&y_1&y_2&\cdots \\ \end{array}\end{displaymath}$

then the entries in this table are (apparently) Laurent polynomials in the x_j and y_j in which every monomial has coefficient +1. Thus b_n counts the number of monomials in this polynomial.
It satisfies the relation

$\begin{displaymath} \det \left( \matrix{ b_{n\hphantom{+0}} & b_{n+1} & b_{n+2} ... ... & b_{n+3} & b_{n+4} } \right) = 1 \hbox{ for all $n \ge 0$ }. \end{displaymath}$ (1)

This property is actually equivalent to the recurrence relation above; see David Speyer's writeup on the $3 \times 3$ determinant recurrence.
We can write b_n = c_n c_n+1, where $\{c_n\}$ is a new sequence defined by

$\begin{displaymath}c_0 = c_1 = c_2 = 1, \quad c_{n} c_{n+3} = c_{n+1} c_{n+2} + 1 \hbox{ for $n \ge 0$ }, \end{displaymath}$

which begins 1, 1, 1, 2, 3, 7, 11, 26, .... This sequence counts several things: for example, c_2n is the number of domino tilings of a $3 \times (2n)$ rectangle. Again, see Speyer's writeup for more details.
The sequence $\{b_n\}$ also satisfies a linear recurrence

b_n = 5b_n-1 - 5b_n-2 + b_n-3

and hence has a rational generating function

$\begin{displaymath}B(x) = \frac{1 - 3x + x^2}{-1 + 5x - 5x^2 + x^3} = \frac{1 - 3x + x^2}{(x - 1)(1 - 4x + x^2)}.\end{displaymath}$

What is the combinatorial interpretation?

Construct an infinite ladder graph G shown below; then b_n gives the number of paths in this graph from P₀ to P_n moving only up and to the right (or moving to the left, in the drawing on the right).

               P_4     .                                          
                  +-+ .                                           
             P_3  | |.                     P_0 P_1 P_2 P_3 P_4    
                +-+-+-+                     *   *   *   *   *     
           P_2  | |/| |                    / \ / \ / \ / \ / \    
              +-+-+-+-+                   *   *   *   *   *   *   
         P_1  | |/| |                      \ / \ / \ / \ / \ /    
            +-+-+-+-+                   ... *---*---*---*---* ... 
       P_0  | |/| |                        / \ / \ / \ / \ / \    
          +-+-+-+-+                       *   *   *   *   *   *   
          | |/| |                          \ / \ / \ / \ / \ /    
          +-+-+-+                           *   *   *   *   *     
           .| |                                                   
          . +-+                                                   
         .

Why does it work?

I'll complete this section later, but for now, just an sketch of the proof: We prove the $3 \times 3$ determinant relation (1) by applying the Gessel-Viennot Theorem (ref?) to the graph above with left endpoints (P₀, P₁, P₂) and right endpoints (P_n+4, P_n+3, P_n+2). The key point is that there exists exactly one way of joining P₀ to P_n+4, P₁ to P_n+3 and P₂ to P_n+2 by three vertex-disjoint paths in G. This determinant relation together with the initial cases b₀ = b₁ = 1, b₂ = 2, b₃ = 6 (which can be checked by hand) uniquely determine the sequence b_n.

What does it mean?

The one-dimensional nature of the paths counted by b_n makes it clear that the sequence, originally defined by a quadratic recurrence, will in fact satisfy a linear recurrence. Looking at the drawing of G on the left, if we define a 5-tuple p_n as the number of paths from P₀ to each of the five vertices on the row containing P_n, then there exists a fixed matrix M such that p_n+1 = Mp_n; the Cayley-Hamilton theorem then tells us that the p_n satisfy a linear recurrence.
As mentioned above, b_n counts the monomials appearing in the Laurent polynomials given by the ``number fence'' recurrence $E = \frac{BD + C}A$ ; a combinatorial understanding of the sequence $\{b_n\}$ is thus a natural first step in understanding the combinatorics of this recurrence relation.