The Benzel Tilings Site

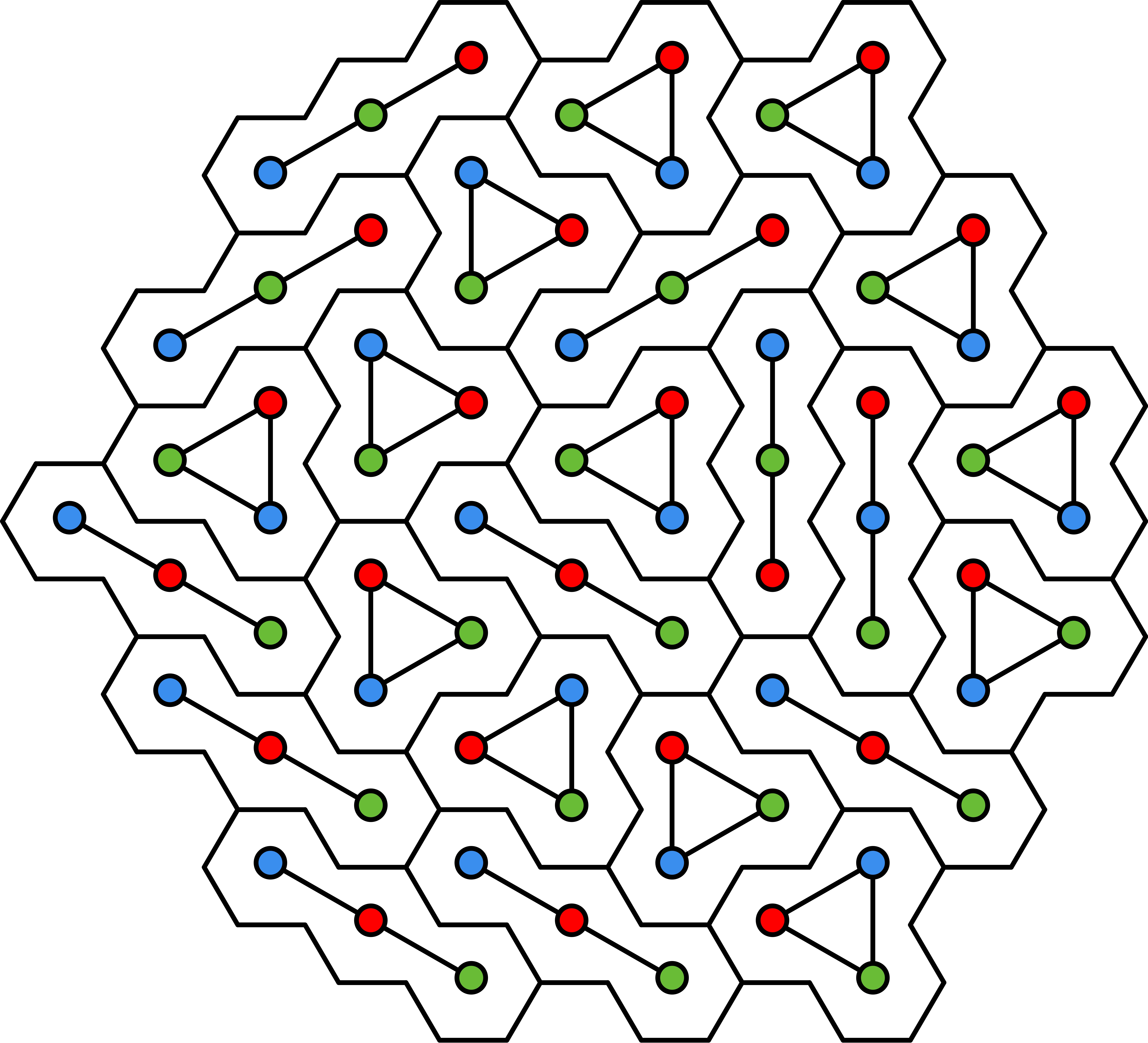
Benzels are regions in the hexagonal grid that are analogous to Aztec diamonds in the square grid vis-a-vis the theory of tilings. Here is an example of a benzel that has been tiled by trihexes (unions of three adjacent hexagonal cells):

(The picture has been superimposed with its graph theoretic dual in which cells become vertices and tiles become collections of edges connecting nearby vertices.)

I gave my first talk on benzels online on November 29, 2021 as part of the CAP21 (Combinatorics and Arithmetic for Physics) workshop sponsored by IHES. (I had only two hours to throw the talk together, so please forgive the lack of slides!) The talk was called "Conjectural Enumerations of Trimer Covers of Finite Subgraphs of the Triangular Lattice" and the video is available on YouTube.

In 2022 I gave several talks about trihex tilings of benzels:

• "Tiling problems, old and new", Rutgers, Mar 30, 2022, with slides and video;
• "Trimer covers in the triangular grid", Open Problems in Algebraic Combinatorics, May 18, 2022, with slides and video; and
• "A pentagonal number theorem for tribone tilings", Michigan State University Combinatorics Seminar, Nov. 2, 2022, with slides and video.

In addition, the following writeups are available:

• Trimer covers in the triangular grid: twenty mostly open problems", to appear in the Proceedings of the 2022 Conference on Open Problems in Algebraic Combinatorics;
• A pentagonal number theorem for tribone tilings (with Jesse Kim), Electronic Journal of Combinatorics 30(3) (2023), #P3.26; and
• Tilings of benzels via the abacus bijection (with Colin Defant, Rupert Li, and Benjamin Young), Combinatorial Theory 3 (2) (2023), #16.
• Tilings of benzels via generalized compression (with Colin Defant, Leigh Foster, Rupert Li, and Benjamin Young), preprint
• Solution of some tiling open problems of Propp, Lai, and some related results (by Seok Hyun Byun, Mihai Ciucu, and Yi-Lin Lee)

Regarding the twenty open problems mentioned in "Trimer covers in the triangular grid", there has been progress on about half of them as of January 2024. In particular:

• Problem 1: Open.
• Problem 2: Solved (DLPY).
• Problem 3: Solved (DLPY).
• Problem 4: Open.
• Problem 5: Solved (DFLPY).
• Problem 6: Open.
• Problem 7: Open.
• Problem 8: Solved (BCL).
• Problem 9: Solved (BCL).
• Problem 10: Solved (BCL).
• Problem 11: Solved (BCL).
• Problem 12: Solved (DFLPY).
• Problem 13: Solved (DFLPY).
• Problem 14: Open.
• Problem 15: Open.
• Problem 16: Open.
• Problem 17: Open.
• Problem 18: Open.
• Problem 19: Open.
• Problem 20: Open.

I coined the term "benzel" in 2021 in honor of the chemical element benzene (whose hexagonal structure reflects the hexagonal cells of which benzels are composed), the Mercedes-Benz car company (whose logo is reminiscent of the way three hexagonal cells meet), the inventor Gustav Benzel (whose 1870 innovation, the merry-go-round, undergoes rotation in a manner vaguely reminiscent of the three-fold rotational symmetry of benzels), and author Carl Sagan (whose novel Contact introduced the word "benzel" as the name of a spinning gadget of extraterrestrial design).