Absolute stability is about the stability of a system with a
uncertain
nonlinear component
(possibly with time-varying uncertainties):
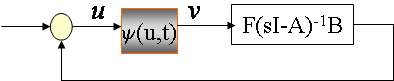
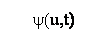 In
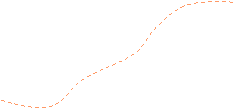
classic absolute stability theory, the function
y(u,t) describing the
uncertain
nonlinear
component
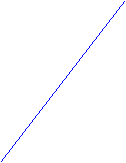
(dashed curves) is bounded by a conic sector
(formed by
two straight lines
v =k1u and v=k2u):
             
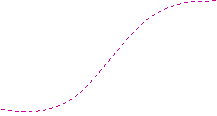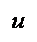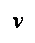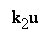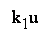
The system is said to be absolutely stable if the
origin is globally stable for any
y(u,t)
within
the conic sector.
Sufficient conditions for absolute stability have
been
obtained via
linear systems
corresponding
to the linear functions bounding the conic
sector. Popular
conditions
are the Circle
Criterion and the Popov Criterion.
|
|
 Motivation for a more flexible sector: In many situations,
we know some
properties
about the nonlinear component. With a particular type
of nonlinearity,
e.g., saturation or
dead-zone, a conic sector might be too
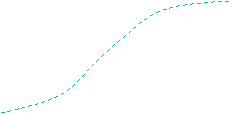
conservative. It is clear
that a pair of piecewise
linear functions can form a tighter
envelope:
The
question is:
1. Are envelopes with piecewise linear boundaries
numerically tractable?
2. How to use a tighter envelope to
improve stability analysis results?
These problems are addressed in the following papers:
-
T. Hu, B. Huang and Z. Lin, ``Absolute stability with a generalized sector
condition,"
IEEE Transactions on Automatic Control, Vol. 49, pp.535-548, 2004.
-
T. Hu and Z. Lin, ``Absolute stability analysis of discrete-time systems with
composite quadratic Lyapunov functions," IEEE Transactions on Automatic
Control, Vol.50, pp.781-797, 2005.
In
these papers, numerically tractable methods are derived for
stability analysis of systems
whose uncertain nonlinearities are bounded by a pair of
piecewise linear functions. If
the piecewise linear functions are
convex/concave, necessary and sufficient conditions
are obtained for quadratic stability.
These conditions are interpreted with Linear Matrix
Inequalities (LMIs) which are
easily solvable with numerical tools. These tools will help the
design of more
efficient dynamic control systems. The main idea and key steps can be found
in the
power point file:
|
