Skip to main content
Logo image

Applied Discrete Structures

Al Doerr, Ken Levasseur

Section 11.6 Direct Products

Subsection 11.6.1 Definition

Our second universal algebraic concept lets us look in the opposite direction from subsystems. Direct products allow us to create larger systems. In the following definition, we avoid complicating the notation by not specifying how many operations the systems have.

Definition 11.6.1. Direct Product.

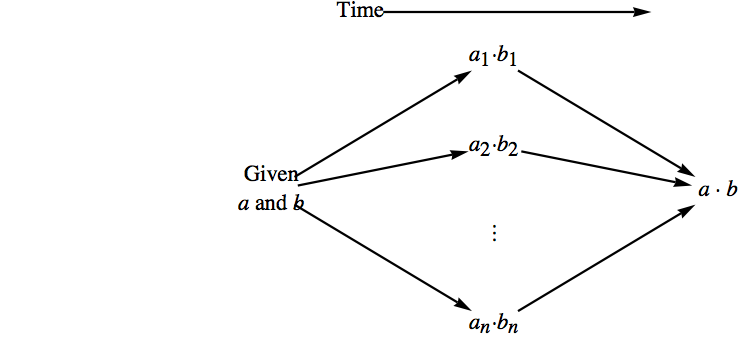
If \(\left[V_i;*_i, \diamond_i, \ldots \right]\text{,}\) \(i = 1, 2, \ldots, n\) are algebraic systems of the same kind, then the direct product of these systems is \(V =V_1\times V_2\times \cdots \times V_n\) , with operations defined below. The elements of \(V\) are \(n\)-tuples of the form \(\left(a_1, a_2, \dots , a _n \right)\text{,}\) where \(a_k \in V_k\text{,}\) \(k = 1, \dots , n\text{.}\) The systems \(V_1\text{,}\) \(V_2, \dots, V_n\) are called the factors of \(V\text{.}\) There are as many operations on \(V\) as there are in the factors. Each of these operations is defined componentwise:
If \(\left(a_1, a_2, . . . , a _n \right), \left(b_1,b_2, . . . , b _n \right)\in V\text{,}\)
\begin{equation*} \begin{array}{c} \left(a_1, a_2, \dots , a_n \right) * \left(b_1, b_2, \dots , b_n \right) = \left(a_1 *_1 b_1, a_2 *_2 b_2,\ldots , a_n *_n b_n \right)\\ \left(a_1, a_2, \dots , a_n \right) \diamond \left(b_1, b_2, \dots , b_n \right) = \left(a_1 \diamond_1 b_1, a_2 \diamond_2 b_2,\dots , a_n \diamond_n b_n\right)\\ \textrm{etc.}\\ \\ \end{array} \end{equation*}
Consider the monoids \(\mathbb{N}\) (the set of natural numbers with addition) and \(B^*\) (the set of finite strings of 0’s and 1’s with concatenation). The direct product of \(\mathbb{N}\) with \(B^*\) is a monoid. We illustrate its operation, which we will denote by \(*\text{,}\) with examples:
\begin{equation*} \begin{array}{c} (4, 001) * (3, 11) = (4 + 3, 001+11) = (7, 00111)\\ (0, 11010) * (3,01) = (3, 1101001)\\ (0, \lambda ) * (129, 00011) = (0 + 129, \lambda +00011) = (129, 00011)\\ (2, 01) * (8, 10) = (10,0110)\textrm{, and }\\ (8, 10) * (2, 01) = (10, 1001) \end{array} \end{equation*}
Note that our new monoid is not commutative. What is the identity for \(*\) ?
The definiton of a Direct Product is quite general and may be confusing to some. Here is the definiton of the direct product of two groups. The definition extends easily to the direct product of three or more groups.

Definition 11.6.3. Direct Product of Two Groups.

Let \([G_1;*_1]\) and \([G_2;*_2]\) be two groups. Their direct product is the system \([G_1 \times G_2; *]\) with domain equal to the Cartesian product of the domains of the two groups and with the coordinatewise operation \(*\) defined by
\begin{equation*} (a_1,b_1)*(a_2,b_2)= (a_1 *_1 a_2, b_1 *_2 b_2) \end{equation*}
for \((a_1,b_1), (a_2,b_2) \in G_1 \times G_2\text{.}\)
Concurrent calculation in a direct product
Figure 11.6.4. Concurrent calculation in a direct product

Note 11.6.5.

  1. On notation. If two or more consecutive factors in a direct product are identical, it is common to combine them using exponential notation. For example, \(\mathbb{Z} \times \mathbb{Z} \times \mathbb{R}\) can be written \(\mathbb{Z}^2 \times \mathbb{R}\text{,}\) and \(\mathbb{R} \times \mathbb{R} \times \mathbb{R} \times \mathbb{R}\) can be written \(\mathbb{R}^4\text{.}\) This is purely a notational convenience; no exponentiation is really taking place.
  2. We call the operations in a direct product componentwise operations, and they are indeed operations on \(V\text{.}\) If two \(n\)-tuples, \(a\) and \(b\text{,}\) are selected from \(V\text{,}\) the first components of \(a\) and \(b\text{,}\) \(a_1\) and \(b_1\text{,}\) are operated on with \(*_1\) to obtain \(a_1*_1b_1\text{,}\) the first component of \(a * b\text{.}\) Note that since \(*_1\) is an operation on \(V_1\text{,}\) \(a_1*_1b_1\) is an element of \(V_1\text{.}\) Similarly, all other components of \(a * b\text{,}\) as they are defined, belong to their proper sets.
  3. One significant fact about componentwise operations is that the components of the result can all be computed at the same time (concurrently). The time required to compute in a direct product can be reduced to a length of time that is not much longer than the maximum amount of time needed to compute in the factors.
  4. A direct product of algebraic systems is not always an algebraic system of the same type as its factors. This is due to the fact that certain axioms that are true for the factors may not be true for the set of \(n\)-tuples. This situation does not occur with groups however. You will find that whenever a new type of algebraic system is introduced, call it type \(T\text{,}\) one of the first theorems that is usually proven, if possible, is that the direct product of two or more systems of type \(T\) is a system of type \(T\text{.}\)

Subsection 11.6.2 Direct Products of Groups

We will explore properties of direct products of groups and examine some concrete examples
We will only present the proof of this theorem for the direct product of two groups. Some slight revisions can be made to produce a proof for any number of factors.
Stating that the direct product of two groups is a group is a short way of saying that if \(\left[G_1; *_1\right]\) and \(\left[G_2; *_2\right]\) are groups, then \(\left[G_1\times G_2; * \right]\) is also a group, where \(*\) is the componentwise operation on \(G_1\times G_2\text{.}\) Associativity of \(*\) : If \(a, b, c \in G_1\times G_2\text{,}\)
\begin{equation*} \begin{split} a * (b * c) & =\left(a_1,a_2\right)*\left(\left(b_1,b_2\right)*\left(c_1,c_2\right)\right)\\ & =\left(a_1,a_2\right)*\left(b_1*_1c_1,b_2*_2c_2\right)\\ & = \left(a_1*_1\left(b_1*_1c_1\right),a_2*_2\left(b_2*_2c_2\right)\right)\\ & = \left(\left(a_1*_1b_1\right)*_1c_1,\left(a_2*_2b_2\right)*_2c_2\right)\\ & = \left(a_1*_1b_1,a_2*_2b_2\right)*\left(c_1,c_2\right)\\ & = \left(\left(a_1,a_2\right)*\left(b_1,b_2\right)\right)*\left(c_1,c_2\right)\\ & = (a * b)*c\\ \end{split} \end{equation*}
Notice how the associativity property hinges on the associativity in each factor. An identity for \(*\text{:}\) As you might expect, if \(e_1\) and \(e_2\) are identities for \(G_1\) and \(G_2\text{,}\) respectively, then \(e = \left(e_1, e _2 \right)\) is the identity for \(G_1 \times G_2\text{.}\) If \(a \in G_1\times G_2\text{,}\)
\begin{equation*} \begin{split} a * e &=\left(a_1,a_2\right)* \left(e_1, e _2 \right)\\ & = \left(a_1*_1e_1,a_2*_2 e _2\right)\\ & = \left(a_1,a_2\right) = a \end{split} \end{equation*}
Similarly, \(e * a = a\text{.}\)
Inverses in \(G_1\times G_2\text{:}\) The inverse of an element is determined componentwise \(a^{-1}= \left(a_1,a_2\right){}^{-1}=\left(a_1{}^{-1},a_2{}^{-1}\right)\text{.}\) To verify, we compute \(a * a^{-1}\) :
\begin{equation*} \begin{split} a * a^{-1} &=\left(a_1,a_2\right)*\left(a_1{}^{-1},a_2{}^{-1}\right)\\ & =\left(a_1*_1a_1{}^{-1},a_2*_2a_2{}^{-1}\right)\\ & = \left(e_1, e _2 \right) =e \end{split} \end{equation*}
Similarly, \(a^{-1} * a=e\text{.}\)
  1. If \(n \geq 2\text{,}\) \(\mathbb{Z}_2{}^n\) , the direct product of \(n\) factors of \(\mathbb{Z}_2\text{,}\) is a group with \(2^n\) elements. We will take a closer look at \(\mathbb{Z}_2{}^3 = \mathbb{Z}_2 \times \mathbb{Z}_2 \times \mathbb{Z}_2\text{.}\) The elements of this group are triples of zeros and ones. Since the operation on \(\mathbb{Z}_2\) is \(+_2\text{,}\) we will use the symbol + for the operation on \(\mathbb{Z}_2{}^3\) . Two of the eight triples in the group are \(a = (1, 0, 1)\) and \(b = (0, 0, 1)\text{.}\) Their “sum” is \(a + b = \left(1 +_2 0, 0 +_2 0, 1 +_2 1\right) = (1, 0, 0)\text{.}\) One interesting fact about this group is that each element is its own inverse. For example \(a + a = (1, 0, 1) + (1, 0, 1) = (0, 0, 0)\text{;}\) therefore \(-a = a\text{.}\) We use the additive notation for the inverse of \(a\) because we are using a form of addition. Note that \(\{(0, 0, 0), (1, 0, 1)\}\) is a subgroup of \(\mathbb{Z}_2{}^3\text{.}\) Write out the “addition” table for this set and apply Theorem 11.5.5. The same can be said for any set consisting of (0, 0, 0) and another element of \(\mathbb{Z}_2{}^3\text{.}\)
  2. The direct product of the positive real numbers with the integers modulo 4, \(\mathbb{R}^+ \times \mathbb{Z}_4\) is an infinite group since one of its factors is infinite. The operations on the factors are multiplication and modular addition, so we will select the neutral symbol \(\diamond\) for the operation on \(\mathbb{R}^+ \times \mathbb{Z}_4\text{.}\) If \(a = (4, 3)\) and \(b = (0.5, 2)\text{,}\) then
    \begin{equation*} \begin{array}{c} a \diamond b = (4, 3) \diamond (0.5, 2) = \left(4 \cdot 0.5, 3 +_4 2\right) = (2, 1)\\ b^2 = b \diamond b = (0.5, 2) \diamond (0.5, 2) = (0.25, 0)\\ a^{-1} = \left(4^{-1} , -3\right) = (0.25, 1)\\ b^{-1} = \left(0.5^{-1} , -2\right) = (2, 2) \end{array} \end{equation*}
    It would be incorrect to say that \(\mathbb{Z}_4\) is a subgroup of \(\mathbb{R}^+\times \mathbb{Z}_4\) , but there is a subgroup of the direct product that closely resembles \(\mathbb{Z}_4\text{.}\) It is \(\{(1, 0), (1, 1), (1, 2), (1, 3)\}\text{.}\) Its table is
    \begin{equation*} \begin{array}{c|cccc} \diamond &(1, 0)& (1, 1)& (1, 2)& (1, 3)\\ \hline (1, 0)&(1, 0)& (1, 1)& (1, 2)& (1, 3)\\ (1, 1)&(1, 1)& (1, 2)& (1, 3)& (1, 0)\\ (1, 2)&(1, 2)& (1, 3)& (1, 0)& (1, 1)\\ (1, 3)&(1, 3)& (1, 0)& (1, 1)& (1, 2)\\ \end{array} \end{equation*}
    Imagine erasing \((1, )\) throughout the table and writing \(+_4\) in place of \(\diamond\text{.}\) What would you get? We will explore this phenomenon in detail in the next section.
    The whole direct product could be visualized as four parallel half-lines labeled 0, 1, 2, and 3 as in Figure 11.6.8. On the \(k\)th line, the point that lies \(x\) units to the right of the zero mark would be \((x,k)\text{.}\) The set \(\{(2^n, (n)1) \mid n \in \mathbb{Z}\}\text{,}\) which is depicted on the figure is a subgroup of \(\mathbb{R}^+\times \mathbb{Z}_4\text{.}\) What cyclic subgroup is it?
    The answer: \(\langle (2, 1)\rangle\) or \(\langle(1/2, 3)\rangle\text{.}\) There are two different generators.
Visualization of the group \(\mathbb{R}^+ \times \mathbb{Z}_4\)
Figure 11.6.8. Visualization of the group \(\mathbb{R}^+ \times \mathbb{Z}_4\)
A more conventional direct product is \(\mathbb{R}^2\text{,}\) the direct product of two factors of \([\mathbb{R}; + ]\text{.}\) The operation on \(\mathbb{R}^2\) is componentwise addition; hence we will use + as the operation symbol for this group. You should be familiar with this operation, since it is identical to addition of \(2 \times 1\) matrices. The Cartesian coordinate system can be used to visualize \(\mathbb{R}^2\) geometrically. We plot the pair \((s, t)\) on the plane in the usual way: \(s\) units along the \(x\) axis and \(t\) units along the \(y\) axis. There is a variety of different subgroups of \(\mathbb{R}^2\) , a few of which are:
  1. \(\{(x, 0) \mid x \in \mathbb{R}\}\text{,}\) all of the points on the \(x\) axis;
  2. \(\{(x, y) \mid 2x- y = 0\}\text{,}\) all of the points that are on the line 2x - y = 0;
  3. If \(a, b \in \mathbb{R}\text{,}\) \(\{(x, y) \mid a x + b y = 0\}\text{.}\) The first two subgroups are special cases of this one, which represents any line that passes through the origin.
  4. \(\{(x, y) \mid 2x - y = k, k \in \mathbb{Z}\}\text{,}\) a union of a set of lines that are parallel to \(2x - y = 0\text{.}\)
  5. \(\{(n, 3n) \mid n \in \mathbb{Z}\}\text{,}\) which is the only countable subgroup that we have listed.
We will leave it to the reader to verify that these sets are subgroups. We will only point out how the fourth example, call it \(H\text{,}\) is closed under “addition.” If \(a = (p, q)\) and \(b = (s, t)\) and both belong to \(H\text{,}\) then \(2p - q = j\) and \(2s - t= k\text{,}\) where both \(j\) and \(k\) are integers. \(a + b = (p, q) + (s, t) = (p + s, q + t)\) We can determine whether \(a + b\) belongs to \(H\) by deciding whether or not \(2(p + s) - (q + t)\) is an integer:
\begin{equation*} \begin{split} 2(p + s) - (q + t) &= 2p + 2s - q - t\\ & = (2p - q) + (2s - t) \\ & = j + k \end{split} \end{equation*}
Since \(j\) and \(k\) are integers, so is \(j +k\text{.}\) This completes a proof that \(H\) is closed under the operation of \(\mathbb{R}^2\text{.}\)
Several useful facts can be stated in regards to the direct product of two or more groups. We will combine them into one theorem, which we will present with no proof. Parts a and c were derived for \(n = 2\) in the proof of Theorem 11.6.6.
Not all subgroups of a direct product can be created using part e of Theorem 11.6.9. For example, \(\{(n, n) \mid n \in \mathbb{Z}\}\) is a subgroup of \(\mathbb{Z}^2\text{,}\) but is not a direct product of two subgroups of \(\mathbb{Z}\text{.}\)
Using the identity \((x + y) + x = y\text{,}\) in \(\mathbb{Z}_2\text{,}\) we can devise a scheme for representing a symmetrically linked list using only one link field. A symmetrically linked list is a list in which each node contains a pointer to its immediate successor and its immediate predecessor (see Figure 11.6.11). If the pointers are \(n\)-digit binary addresses, then each pointer can be taken as an element of \(\mathbb{Z}_2{}^n\text{.}\) Lists of this type can be accomplished using cells with only one link. In place of a left and a right pointer, the only “link” is the value of the sum (left link) + (right link). All standard list operations (merge, insert, delete, traverse, and so on) are possible with this structure, provided that you know the value of the nil pointer and the address, \(f\text{,}\) of the first (i. e., leftmost) cell. Since first \(f.\textrm{ left}\) is nil, we can recover \(f.\textrm{ right}\) by adding the value of nil: \(f + \textrm{ nil} = (\textrm{ nil} + f.\textrm{right}) + \textrm{nil} = f.\textrm{right}\text{,}\) which is the address of the second item. Now if we temporarily retain the address, \(s\text{,}\) of the second cell, we can recover the address of the third item. The link field of the second item contains the sum \(s.\textrm{ left} + s.\textrm{ right} = \textrm{ first} + \textrm{ third}\text{.}\) Therefore
\begin{equation*} \begin{split} (\textrm{first} + \textrm{third})+ \textrm{first} &= s + s.\textrm{left}\\ &=( s.\textrm{left} + s.\textrm{right})+ s.\textrm{left}\\ &=s.\textrm{right}\\ &= \textrm{third} \end{split} \end{equation*}
We no longer need the address of the first cell, only the second and third, to recover the fourth address, and so forth.
Symmetric Linked Lists
Figure 11.6.11. Symmetric Linked Lists
The following more formal algorithm uses names that reflects the timing of the visits.
Given a symmetric list, a traversal of the list is accomplished as follows, where \(\textit{first}\) is the address of the first cell. We presume that each item has some information that is represented by \(\textrm{item}.\textrm{info}\) and a field called item.link that is the sum of the left and right links.
Table 11.6.12.
(1) yesterday =nil
(2) today =first
(3)\(\quad \)while \(\textrm{today} \neq \textrm{nil}\text{:}\)
\(\quad \quad \quad \)(3.1)Write(today.info)
\(\quad \quad \quad \)(3.2)tomorrow = today.link + yesterday
\(\quad \quad \quad \)(3.3)yesterday = today
\(\quad \quad \quad \)(3.4)today = tomorrow.
At any point in this algorithm it would be quite easy to insert a cell between today and tomorrow. Can you describe how this would be accomplished?
This implementation of doubly linked lists is often referred to as an XOR linked list. For more information see the Wikipedia page en.wikipedia.org/wiki/XOR_linked_list.

Exercises 11.6.3 Exercises

1.

Write out the group table of \(\mathbb{Z}_2 \times \mathbb{Z}_3\) and find the two proper subgroups of this group.
Answer.
Table of \(\mathbb{Z}_2\times \mathbb{Z}_3\text{:}\)
\begin{equation*} \begin{array}{c|cccccc} +&(0,0)&(0,1)&(0,2)&(1,0)&(1,1)&(1,2)\\ \hline (0,0)&(0,0)&(0,1)&(0,2)&(1,0)&(1,1)&(1,2)\\ (0,1)&(0,1)&(0,2)&(0,0)&(1,1)&(1,2)&(1,0)\\ (0,2)&(0,2)&(0,0)&(0,1)&(1,2)&(1,0)&(1,1)\\ (1,0)&(1,0)&(1,1)&(1,2)&(0,0)&(0,1)&(0,2)\\ (1,1)&(1,1)&(1,2)&(1,0)&(0,1)&(0,2)&(0,0)\\ (1,2)&(1,2)&(1,0)&(1,1)&(0,2)&(0,0)&(0,1) \end{array} \end{equation*}
The only two proper subgroups are \(\{(0, 0), (1, 0)\}\) and \(\{(0, 0), (0, 1), (0, 2)\}\)

2.

List more examples of proper subgroups of \(\mathbb{R}^2\) that are different from the ones listed in this section.

3. Algebraic properties of the \(n\)-cube.

  1. The four elements of \(\mathbb{Z}_2{}^2\) can be visualized geometrically as the four corners of the 2-cube. Algebraically describe the statements:
    1. Corners \(a\) and \(b\) are adjacent.
    2. Corners \(a\) and \(b\) are diagonally opposite one another.
  2. The eight elements of \(\mathbb{Z}_2{}^3\) can be visualized as the eight corners of the 3-cube. One face contains \(\mathbb{Z}_2 \times \mathbb{Z}_2\times \{0\}\) and the opposite face contains the remaining four elements so that \((a, b, 1)\) is behind \((a, b, 0)\text{.}\) As in part a, describe statements i and ii algebraically.
  3. If you could imagine a geometric figure similar to the square or cube in \(n\) dimensions, and its corners were labeled by elements of \(\mathbb{Z}_2{}^n\) as in parts a and b, how would statements i and ii be expressed algebraically?
Answer.
  1. (i) \(a + b \textrm{ could be }(1, 0) \textrm{ or } (0, 1)\text{.}\) (ii) \(a + b = (1, 1)\text{.}\)
  2. (i) \(a + b \textrm{ could be}(1, 0, 0), (0, 1, 0), \textrm{ or }(0, 0, 1)\text{.}\) (ii) \(a + b = (1, 1, 1)\text{.}\)
  3. (i) \(a + b\) has exactly one 1. (ii) \(a + b\) has all \(1's\text{.}\)

4.

  1. Suppose that you were to be given a group \([G; * ]\) and asked to solve the equation \(x * x = e\text{.}\) Without knowing the group, can you anticipate how many solutions there will be?
  2. Answer the same question as part a for the equation \(x * x = x\text{.}\)

5.

Which of the following sets are subgroups of \(\mathbb{Z} \times \mathbb{Z}\text{?}\) Give a reason for any negative answers.
  1. \(\displaystyle \{0\}\)
  2. \(\displaystyle \{(2j, 2k) \mid j,k\in \mathbb{Z}\}\)
  3. \(\displaystyle \{(2j+ 1, 2k) \mid j,k\in \mathbb{Z}\}\)
  4. \(\displaystyle \{(n, n^2 ) \mid n \in \mathbb{Z}\}\)
  5. \(\displaystyle \{(j, k) \mid j + k\textrm{ is} \textrm{ even}\}\)
Answer.
  1. No, 0 is not an element of \(\mathbb{Z} \times \mathbb{Z}\text{.}\)
  2. Yes.
  3. No, (0, 0) is not an element of this set.
  4. No, the set is not closed: \((1, 1) + (2, 4) = (3, 5)\) and \((3, 5)\) is not in the set.
  5. Yes.

6.

Determine the following values in the group \(\mathbb{Z}_3 \times \mathbb{R}^*\text{:}\)
  1. \(\displaystyle (2,1)* (1,2)\)
  2. the identity element
  3. \(\displaystyle (1, 1/2)^{-1}\)
<Prev^TopNext>