Applied Discrete Structures

Let \(p_1= \left(e_1, e_2, \ldots , e_m \right)\) and \(p_2=\left(f_1,f_2,\ldots , f_n\right)\) be two different simple paths from \(v_a\) to \(v_b\text{.}\) The first step we will take is to delete from \(p_1\) and \(p_2\) the initial edges that are identical. That is, if \(e_1= f_1\text{,}\) \(e_2= f_2, \dots \text{,}\) \(e_{j}= f_j\text{,}\) and \(e_{j+1}\neq f_{j+1}\) delete the first \(j\) edges of both paths. Once this is done, both paths start at the same vertex, call it \(v_c\text{,}\) and both still end at \(v_b\text{.}\) Now we construct a cycle by starting at \(v_c\) and following what is left of \(p_1\) until we first meet what is left of \(p_2\text{.}\) If this first meeting occurs at vertex \(v_d\text{,}\) then the remainder of the cycle is completed by following the portion of the reverse of \(p_2\) that starts at \(v_d\) and ends at \(v_c\text{.}\)

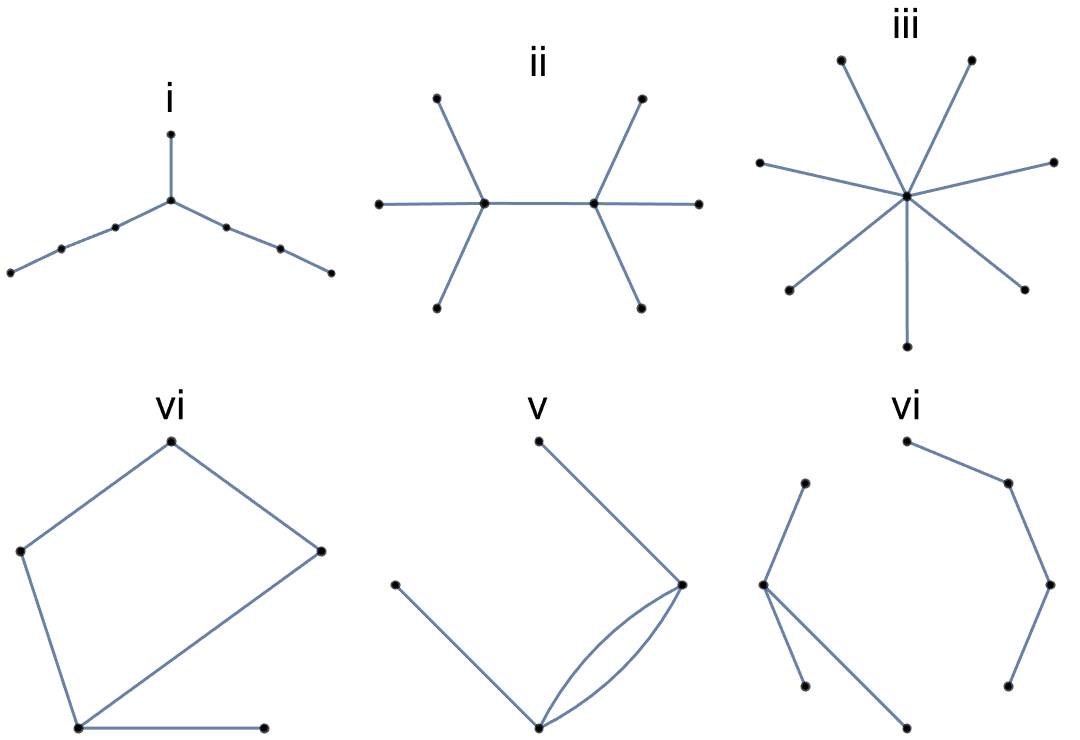
Proof Strategy. Most of this theorem can be proven by proving the following chain of implications: \((1) \Rightarrow (2)\text{,}\) \((2) \Rightarrow (3)\text{,}\) \((3)\Rightarrow (4)\text{,}\) and \((4) \Rightarrow (1)\text{.}\) Once these implications have been demonstrated, the transitive closure of \(\Rightarrow\) on \({1, 2, 3, 4}\) establishes the equivalence of the first four conditions. The proof that Statement 5 is equivalent to the first four can be done by induction, which we will leave to the reader.

\((1) \Rightarrow (2)\) (Indirect). Assume that \(G\) is a tree and that there exists a pair of vertices between which there is either no path or there are at least two distinct paths. Both of these possibilities contradict the premise that \(G\) is a tree. If no path exists, \(G\) is disconnected, and if two paths exist, a cycle can be obtained by Theorem 10.1.11.

\((2) \Rightarrow (3)\text{.}\) We now use Statement 2 as a premise. Since each pair of vertices in \(V\) are connected by exactly one path, \(G\) is connected. Now if we select any edge \(e\) in \(E\text{,}\) it connects two vertices, \(v_1\) and \(v_2\text{.}\) By (2), there is no simple path connecting \(v_1\) to \(v_2\) other than \(e\text{.}\) Therefore, no path at all can exist between \(v_1\) and \(v_2\) in \((V, E - \{e\})\text{.}\) Hence \((V, E - \{e\})\) is disconnected.

\((3)\Rightarrow (4)\text{.}\) Now we will assume that Statement 3 is true. We must show that \(G\) has no cycles and that adding an edge to \(G\) creates a cycle. We will use an indirect proof for this part. Since (4) is a conjunction, by DeMorgan’s Law its negation is a disjunction and we must consider two cases. First, suppose that \(G\) has a cycle. Then the deletion of any edge in the cycle keeps the graph connected, which contradicts (3). The second case is that the addition of an edge to \(G\) does not create a cycle. Then there are two distinct paths between the vertices that the new edge connects. By Lemma 10.1.10, a cycle can then be created, which is a contradiction.

\((4) \Rightarrow (1)\) Assume that \(G\) contains no cycles and that the addition of an edge creates a cycle. All that we need to prove to verify that \(G\) is a tree is that \(G\) is connected. If it is not connected, then select any two vertices that are not connected. If we add an edge to connect them, the fact that a cycle is created implies that a second path between the two vertices can be found which is in the original graph, which is a contradiction.