Skip to main content
Logo image

Applied Discrete Structures

Al Doerr, Ken Levasseur

Section 8.5 Generating Functions

This section contains an introduction to the topic of generating functions and how they are used to solve recurrence relations, among other problems. Methods that employ generating functions are based on the concept that you can take a problem involving sequences and translate it into a problem involving generating functions. Once you’ve solved the new problem, a translation back to sequences gives you a solution of the original problem.
This section covers:
  1. The definition of a generating function.
  2. Solution of a recurrence relation using generating functions to identify the skills needed to use generating functions.
  3. An introduction and/or review of the skills identified in point 2.
  4. Some applications of generating functions.

Subsection 8.5.1 Definition

Definition 8.5.1. Generating Function of a Sequence.

The generating function of a sequence \(S\) with terms \(S_0,S_1 ,S_2, \dots \text{,}\) is the infinite sum
\begin{equation*} G(S;z)=\sum_{n=0}^{\infty} S_n z^n=S_0+S_1 z+S_2 z^2+S_3 z^3+\cdots \end{equation*}
The domain and codomain of generating functions will not be of any concern to us since we will only be performing algebraic operations on them.
  1. If \(S_n = 3^n\text{,}\)\(n \geq 0\text{,}\) then
    \begin{equation*} \begin{split} G(S;z) &= 1 + 3z + 9z^2 + 27z^3 +\cdots \\ & =\sum_{n=0}^{\infty} 3^n z^n\\ &=\sum_{n=0}^{\infty} (3 z)^n\\ \end{split} \end{equation*}
    We can get a closed form expression for \(G(S;z)\) by observing that \(G(S;z) - 3z G(S;z) = 1\text{.}\) Therefore, \(G(S;z) =\frac{1}{1-3 z}\text{.}\)
  2. Finite sequences have generating functions. For example, the sequence of binomial coefficients \(\binom{n}{0} \text{,}\) \(\binom{n}{1} \text{,}\) \(\ldots\text{,}\)\(\binom{n}{n} \text{,}\) \(n \geq 1\) has generating function
    \begin{equation*} \begin{split} G(\binom{n}{\cdot}; z) & = \binom{n}{0} + \binom{n}{1} z +\cdots + \binom{n}{n} z^n\\ & = \sum_{k=0}^{\infty} \binom{n}{k} z^k\\ &=(1+z)^n\\ \end{split} \end{equation*}
    by application of the binomial formula.
  3. If \(Q(n) = n^2\text{,}\) \(G(Q;z)=\sum_{n=0}^{\infty} n^2 z^n=\sum_{k=0}^{\infty} k^2 z^k\text{.}\) Note that the index that is used in the summation has no significance. Also, note that the lower limit of the summation could start at 1 since \(Q(0)=0\text{.}\)

Subsection 8.5.2 Solution of a Recurrence Relation Using Generating Functions

We illustrate the use of generating functions by solving \(S(n) - 2S(n - 1) - 3S(n - 2) = 0\text{,}\) \(n \geq 2\text{,}\) with \(S(0) = 3\) and \(S(1) = 1\text{.}\)
  1. Translate the recurrence relation into an equation about generating functions.
    Let \(V(n) = S(n) - 2S (n - 1) - 3S (n - 2)\text{,}\) \(n \geq 2\text{,}\) with \(V(0) = 0\) and \(V(1) = 0\text{.}\) Therefore,
    \begin{equation*} G(V;z) = 0 + 0z +\sum_{n=2}^{\infty} (S(n) - 2S (n - 1) - 3S (n - 2)) z^n= 0 \end{equation*}
  2. Solve for the generating function of the unknown sequence, \(G(S;z) = \sum_{n=0}^{\infty} S_n z^n\text{.}\)
    \begin{equation*} \begin{split} 0 & =\sum_{n=2}^{\infty} {(S(n) - 2S (n - 1) - 3 S (n - 2)) z^n}\\ & =\sum_{n=2}^{\infty} {S(n) z^n-2} \left(\sum_{n=2}^{\infty } S(n-1) z^n\right)-3\left(\sum_{n=2}^{\infty} S(n-2) z^n\right) \end{split} \end{equation*}
    Close examination of the three sums above shows:
    1. \begin{equation*} \begin{split} \sum_{n=2}^{\infty} S_n z^n &=\sum_{n=0}^{\infty} S_n z^n - S(0)-S(1)z\\ &= G(S;z)-3-z \end{split} \end{equation*}
      since \(S(0)=3\) and \(S(1)=1\text{.}\)
    2. \begin{equation*} \begin{split} \sum_{n=2}^{\infty} S(n-1) z^n &=z\left(\sum_{n=2}^{\infty} S(n-1) z^{n-1}\right)\\ & =z\left(\sum_{n=1}^{\infty} S(n) z^n\right)\\ & = z\left(\sum_{n=0}^{\infty} S(n) z^n-S(0)\right)\\ &= z(G(S;z)-3) \end{split} \end{equation*}
    3. \begin{equation*} \begin{split} \sum_{n=2}^{\infty} S(n-2) z^n & = z^2\left(\sum_{n=2}^{\infty} S(n-2) z^{n-2}\right)\\ & =z^2G(S;z) \end{split} \end{equation*}
      Therefore,
      \begin{equation*} \begin{split} &(G(S;z)-3-z)-2z(G(S;z)-3)-3z^2G(S;z)=0\\ & \Rightarrow G(S;z)-2z G(S;z)-3z^2G(S;z)=3 - 5z\\ &\Rightarrow G(S;z)=\frac{3-5z}{1-2z-3z^2} \end{split} \end{equation*}
  3. Determine the sequence whose generating function is the one we got in Step 2.
    For our example, we need to know one general fact about the closed form expression of an exponential sequence (a proof will be given later):
    \begin{gather} T(n)=b a^n ,n\geq 0 \Leftrightarrow G(T;z)=\frac{b}{1-a z} \tag{8.5.1} \end{gather}
    Now, in order to recognize \(S\) in our example, we must write our closed form expression for \(G(S;z)\) as a sum of terms like \(G(T;z)\) above. Note that the denominator of \(G(S;z)\) can be factored:
    \begin{equation*} G(S;z)=\frac{3-5z}{1-2z-3z^2} =\frac{3-5z}{(1-3z)(1+z)} \end{equation*}
    If you look at this last expression for \(G(S;z)\) closely, you can imagine how it could be the result of addition of two fractions,
    \begin{gather} \frac{3-5z}{(1-3z)(1+z)} = \frac{A}{1-3z}+ \frac{B}{1+z}\tag{8.5.2} \end{gather}
    where \(A\) and \(B\) are two real numbers that must be determined. Starting on the right of (8.5.2), it should be clear that the sum, for any \(A\) and \(B\text{,}\) would look like the left-hand side. The process of finding values of \(A\) and \(B\) that make (8.5.2) true is called the partial fractions decomposition of the left-hand side:
    \begin{equation*} \begin{split} \frac{A}{1-3z}+ \frac{B}{1+z} &=\frac{A(1+z)}{(1-3z)(1+z)}+ \frac{B(1-3z)}{(1-3z)(1+z)}\\ & =\frac{(A+B)+(A-3B)z}{(1-3z)(1+z)} \end{split} \end{equation*}
    Therefore,
    \begin{equation*} \left\{ \begin{array}{c} A+B=3 \\ A-3B=-5 \\ \end{array} \right\}\Rightarrow \left\{ \begin{array}{c} A=1 \\ B=2 \\ \end{array} \right\} \end{equation*}
    and
    \begin{equation*} G(S;z)= \frac{1}{1-3z}+ \frac{2}{1+z} \end{equation*}
    We can apply (8.5.1) to each term of \(G(S;z)\text{:}\)
    • \(\frac{1}{1-3z}\) is the generating function for \(S_1(n)=1\cdot 3^n= 3^n\)
    • \(\frac{2}{1+z}\) is the generating function for \(S_2(n)=2(-1)^n\text{.}\)
    Therefore, \(S(n)=3^n+ 2(-1)^n\text{.}\)
From this example, we see that there are several skills that must be mastered in order to work with generating functions. You must be able to:
  1. Manipulate summation expressions and their indices (in Step 2).
  2. Solve algebraic equations and manipulate algebraic expressions, including partial function decompositions (Steps 2 and 3).
  3. Identify sequences with their generating functions (Steps 1 and 3).
We will concentrate on the last skill first, a proficiency in the other skills is a product of doing as many exercises and reading as many examples as possible.
First, we will identify the operations on sequences and on generating functions.

Subsection 8.5.3 Operations on Sequences

Definition 8.5.3. Operations on Sequences.

Let \(S\) and \(T\) be sequences of numbers and let \(c\) be a real number. Define the sum \(S + T\text{,}\) the scalar product \(c S\text{,}\) the product \(S T\text{,}\) the convolution \(S*T\text{,}\) the pop operation \(S\uparrow\) (read “\(S\) pop”), and the push operation \(S\downarrow\) (read “\(S\) push”) term-wise for \(k \geq 0\) by
\begin{gather} (S + T)(k) = S(k) + T(k)\tag{8.5.3} \end{gather}
\begin{gather} (c S)(k) = c S(k)\tag{8.5.4} \end{gather}
\begin{gather} (S \cdot T)(k) = S(k)T(k)\tag{8.5.5} \end{gather}
\begin{gather} (S*T)(k) = \sum_{j=0}^k S(j) T(k-j)\tag{8.5.6} \end{gather}
\begin{gather} (S\uparrow )(k) = S(k+1)\tag{8.5.7} \end{gather}
\begin{align} (S\downarrow )(k)=\left\{ \begin{array}{cc} 0 & \textrm{ if } k=0 \\ S(k-1) & \textrm{ if } k>0 \end{array}\right.\tag{8.5.8} \end{align}
If one imagines a sequence to be a matrix with one row and an infinite number of columns, \(S + T\) and \(c S\) are exactly as in matrix addition and scalar multiplication. There is no obvious similarity between the other operations and matrix operations.
The pop and push operations can be understood by imagining a sequence to be an infinite stack of numbers with \(S(0)\) at the top, \(S(1)\) next, etc., as in Figure 8.5.4a. The sequence \(S\uparrow\) is obtained by “popping” S(0) from the stack, leaving a stack as in Figure 8.5.4b, with S(1) at the top, S(2) next, etc. The sequence \(S\downarrow\) is obtained by placing a zero at the top of the stack, resulting in a stack as in Figure 8.5.4c. Keep these figures in mind when we discuss the pop and push operations.
Stack interpretation of pop and push operation
Figure 8.5.4. Stack interpretation of pop and push operation
If \(S(n) = n\text{,}\) \(T(n) = n^2\text{,}\) \(U(n) = 2^n\text{,}\) and \(R(n) =n 2^n\text{:}\)
  1. \(\displaystyle (S + T)(n) = n + n^2\)
  2. \(\displaystyle (U + R)(n) = 2^n+ n 2^n= (1+n)2^n\)
  3. \(\displaystyle (2 U)(n) = 2\cdot 2^n= 2^{n+1}\)
  4. \(\displaystyle \left(\frac{1}{2}R\right)(n)= \frac{1}{2}n 2^n= n 2^{n-1}\)
  5. \(\displaystyle (S\cdot T)(n) = n n^2 = n^3\)
  6. \(\displaystyle (S*T)(n)= \sum_{j=0}^n S(j) T(n-j)= \sum_{j=0}^n j (n-j)^2\\ \\ \quad \quad =\sum_{j=0}^n \left( j n^2-2 n j^2 + j^3\right)\\ \\ \quad \quad = n^2\sum_{j=0}^n j-2n \sum_{j=0}^n j^2 + \sum_{j=0}^n j ^3\\ \\ \quad \quad =n^{2 }\left(\frac{n (n+1)}{2}\right)- 2n\left(\frac{(2n+1)(n+1)n}{6}\right)+\frac{1}{4} n^2 (n+1)^2\\ \\ \quad \quad = \frac{n^2(n+1)(n-1)}{12}\)
  7. \(\displaystyle (U*U)(n) =\sum_{j=0}^n U(j) U(n-j)\\ \\ \quad \quad =\sum_{j=0}^n 2^j 2^{n-j}\\ \\ \quad \quad = (n+1)2^n\)
  8. \(\displaystyle (S\uparrow )(n)=n+1\)
  9. \(\displaystyle (S\downarrow )(n)=\max (0,n-1)\)
  10. \(\displaystyle ((S\downarrow )\downarrow )(n)= \max (0, n - 2)\)
  11. \(\displaystyle (U\downarrow )(n)=\left\{ \begin{array}{cc} 2^{n-1} & \textrm{ if } n>0 \\ 0 & \textrm{ if } n=0 \\ \end{array} \right.\)
  12. \(\displaystyle ((U\downarrow )\uparrow )(n)=(U\downarrow )(n+1)= 2^n= U(n)\)
  13. \(\displaystyle ((U\uparrow )\downarrow ) (n)=\left\{ \begin{array}{cc} 0 & \textrm{ if } n = 0 \\ U(n) & \textrm{ if } n>0 \\ \end{array} \right.\)
Note that \((U\downarrow )\uparrow \neq (U\uparrow )\downarrow\text{.}\)

Definition 8.5.6. Multiple Pop and Push.

If S is a sequence of numbers and \(p\) a positive integer greater than 1, define
\begin{equation*} S\uparrow p = (S\uparrow (p - 1))\uparrow \quad\textrm{ if }p \geq 2 \textrm{ and }S\uparrow 1 = S\uparrow \end{equation*}
Similarly, define
\begin{equation*} S\downarrow p = (S\downarrow (p - 1))\downarrow \quad\textrm{ if } p \geq 2\textrm{ and }S\downarrow 1 = S\downarrow \end{equation*}
In general, \((S \uparrow p)(k) = S(k+p),\) and
\begin{equation*} (S\downarrow p)(k)=\left\{ \begin{array}{cc} 0 & \textrm{ if } k < p \\ S(k-p) & \textrm{ if } k\geq p \\ \end{array} \right. \end{equation*}

Subsection 8.5.4 Operations on Generating Functions

Definition 8.5.7. Operations on Generating Functions.

If \(G(z)=\sum_{k=0}^{\infty} a_k z^k\) and \(H(z) =\sum_{k=0}^{\infty} b_k z^k\) are generating functions and \(c\) is a real number, then the sum \(G + H\text{,}\) scalar product \(c G\text{,}\) product \(G H\text{,}\) and monomial product \(z^p G\text{,}\) \(p \geq 1\) are generating functions, where
\begin{gather} (G + H)(z)=\sum_{k=0}^{\infty} \left(a_k+b_k\right) z^k\tag{8.5.9}\\ (c G)(z)=\sum_{k=0}^{\infty} c a_k z^k\tag{8.5.10}\\ (G H)(z) = \sum_{k=0}^{\infty} c z^k \textrm{ where } c_k= \sum_{j=0}^k a_jb_{k-j}\tag{8.5.11}\\ \left(z^p G\right)(z) = z^p\sum_{k=0}^{\infty} a_k z^k=\sum_{k=0}^{\infty} a_k z^{k+p} = \sum_{n=p}^{\infty} a_{n-p} z^n\tag{8.5.12} \end{gather}
The last sum is obtained by substituting \(n - p\) for \(k\) in the previous sum.
If \(D(z) =\sum_{k=0}^{\infty} kz^k\) and \(H(z) =\sum_{k=0}^{\infty} 2^k z^k\) then
\begin{equation*} (D + H)(z) =\sum_{k=0}^{\infty} \left(k+2^k\right) z^k \end{equation*}
\begin{equation*} (2H)(z)= \sum_{k=0}^{\infty} 2\cdot 2^kz^k =\sum_{k=0}^{\infty} 2^{k+1}z^k \end{equation*}
\begin{equation*} \begin{split} (z D)(z) &= z\sum_{k=0}^{\infty} kz^k= \sum_{k=0}^{\infty} kz^{k+1}\\ &= \sum_{k=1}^{\infty} (k-1) z^k = D(z)- \sum_{k=1}^{\infty} z^k\\ \end{split} \end{equation*}
\begin{equation*} (D H)(z)=\sum_{k=0}^{\infty} \left(\sum_{j=0}^k j 2^{k-j}\right)z^k \end{equation*}
\begin{equation*} (H H)(z)= \sum_{k=0}^{\infty} \left(\sum_{j=0}^k 2^j2^{k-j}\right) z^k=\sum_{k=0}^{\infty} (k+1)2^k z^k \end{equation*}
Note: \(D(z) = G(S;z)\text{,}\) and \(H(z) = G(U;z)\) from Example 5.
Now we establish the connection between the operations on sequences and generating functions. Let \(S\) and \(T\) be sequences and let \(c\) be a real number.
\begin{gather} G(S+T;z)=G(S;z)+G(T;z)\tag{8.5.13}\\ G(cS;z)=c G(S;z)\tag{8.5.14}\\ G(S*T;z)=G(S;z) G(T;z)\tag{8.5.15}\\ G(S\uparrow ;z)=(G(S;z)-S(0))/z\tag{8.5.16}\\ G(S\downarrow ;z)=z G(S;z)\tag{8.5.17} \end{gather}
In words, (8.5.13) says that the generating function of the sum of two sequences equals the sum of the generating functions of those sequences. Take the time to write out the other four identities in your own words. From the previous examples, these identities should be fairly obvious, with the possible exception of the last two. We will prove (8.5.16) as part of the next theorem and leave the proof of (8.5.17) to the interested reader. Note that there is no operation on generating functions that is related to sequence multiplication; that is, \(G(S\cdot T;z)\) cannot be simplified.
We prove (a) by induction and leave the proof of (b) to the reader.
Basis:
\begin{equation*} \begin{split} G(S\uparrow;z) &= \sum_{k=0}^{\infty} S(k+1) z^k\\ & =\sum_{k=1}^{\infty} S(k) z^{k-1}\\ & =\left.\left(\sum_{k=1}^{\infty} S(k) z^k\right)\right/z\\ & =\left.\left(S(0)+\sum_{k=1}^{\infty} S(k) z^k-S(0)\right)\right/z\\ & =(G(S;z)-S(0))/z \end{split} \end{equation*}
Therefore, part (a) is true for \(p=1\text{.}\)
Induction: Suppose that for some \(p\geq 1\text{,}\) the statement in part (a) is true:
\begin{equation*} \begin{split} G(S\uparrow (p+1);z) &= G((S\uparrow p)\uparrow ;z)\\ & = (G(S\uparrow p ;z)-(S\uparrow p)(0))/z \textrm{ by the basis}\\ & = \frac{\frac{\left(G(S;z)-\sum_{k=0}^{p-1} S(k) z^k\right)}{z^p}-S(p)}{z} \end{split} \end{equation*}
by the induction hypothesis. Now write \(S(p)\) in the last expression above as \(\left(S(p)z^p \right)/z^p\) so that it fits into the finite summation:
\begin{equation*} \begin{split} G(S\uparrow (p+1);z) & =\left.\left(\frac{G(S;z)-\sum_{k=0}^p S(k) z^k}{z^p}\right)\right/z\\ & = \left(G(S;z)-\sum_{k=0}^p S(k) z^k\right)/z^{p+1} \end{split} \end{equation*}
Therefore the statement is true for \(p+1\text{.}\)

Subsection 8.5.5 Closed Form Expressions for Generating Functions

The most basic tool used to express generating functions in closed form is the closed form expression for the geometric series, which is an expression of the form \(a + a r + a r^2+ \cdots\text{.}\) It can either be terminated or extended infinitely.
Finite Geometric Series:
\begin{gather} a + a r + a r^2+ \cdots +a r^n= a\left(\frac{1-r^{n+1}}{1-r}\right)\tag{8.5.18} \end{gather}
Infinite Geometric Series:
\begin{gather} a + a r + a r^2+ \cdots = \frac{a}{1-r}\tag{8.5.19} \end{gather}
Restrictions: \(a\) and \(r\) represent constants and the right sides of the two equations apply under the following conditions:
  1. \(r\) must not equal 1 in the finite case. Note that \(a + a r + \cdots a r^n = (n + 1)a\) if \(r = 1\text{.}\)
  2. In the infinite case, the absolute value of \(r\) must be less than 1.
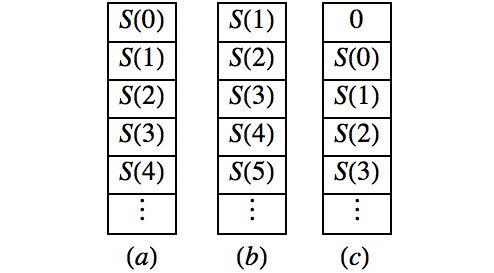
These restrictions don’t come into play with generating functions. We could derive (8.5.18) by noting that if \(S(n) = a + a r +\cdots + a r^n\text{,}\) \(n > 0\text{,}\) then \(S(n) = r S(n - 1) + a\) (See Exercise 10 of Section 8.3). An alternative derivation was used in Section 8.4. We will take the same steps to derive (8.5.19). Let \(x = a + a r + a r^2 + \cdots \text{.}\) Then
\begin{equation*} r x =a r+ ar^2 +\cdots = x- a \Rightarrow x-rx=a \Rightarrow x= \frac{a}{1-r} \end{equation*}
  1. If \(S(n) = 9\cdot 5^n\text{,}\) \(n \geq 0\text{,}\) \(G(S;z)\) is an infinite geometric series with \(a = 9\) and \(r = 5z\text{.}\)Therefore, \(G(S;z) = \frac{9}{1 - 5z}\text{.}\)
  2. If \(T(n) = 4\text{,}\) \(n \geq\)0, then \(G(T;z) = 4/(1 - z)\text{.}\)
  3. If \(U(n) = 3(-1)^n\text{,}\) then \(G(U;z) = 3/(1 + z)\text{.}\)
  4. Let \(C(n) = S(n) + T(n) + U(n) = 9 \cdot 5^n + 4 + 3(-1)^n\text{.}\) Then
    \begin{equation*} \begin{split} G(C;z) & = G(S;z) + G(T;z) + G(U;z)\\ & = \frac{9}{1-5z} + \frac{4}{1-z}+ \frac{3}{1+z}\\ & = -\frac{14 z^2+34z-16}{5 z^3-z^2-5 z+1} \end{split}\text{.} \end{equation*}
    Given a choice between the last form of \(G(C;z)\) and the previous sum of three fractions, we would prefer leaving it as a sum of three functions. As we saw in an earlier example, a partial fractions decomposition of a fraction such as the last expression requires some effort to produce.
  5. If \(G(Q;z) = 34/(2 - 3z)\text{,}\) then \(Q\) can be determined by multiplying the numerator and denominator by 1/2 to obtain \(\frac{17}{1-\frac{3}{2}z}\text{.}\) We recognize this fraction as the sum of the infinite geometric series with \(a = 17\) and \(r = \frac{3}{2}z\text{.}\) Therefore \(Q(n) = 17(3/2)^n\text{.}\)
  6. If \(G(A;z) = (1 + z)^3\) , then we expand \((1 + z)^3\) to \(1 + 3z + 3z^2 + z^{3}\) . Therefore \(A(0) = 1\text{,}\) \(A(1) = 3\) \(A(2)= 3\text{,}\) \(A(3) = 1\text{,}\) and, since there are no higher-powered terms, \(A(n) = 0\text{,}\) \(n \geq 4\text{.}\) A more concise way of describing \(A\) is \(A(k) = \binom{3}{k} \text{,}\) since \(\binom{n}{k} \) is interpreted as 0 of \(k > n\text{.}\)
Table 8.5.11 lists some closed form expressions for the generating functions of some common sequences.
Table 8.5.11. Closed Form Expressions of some Generating Functions
\(\) \(\)
Sequence Generating Function
\(S(k)=b a^k\) \(G(S;z)=\frac{b}{1-a z}\)
\(S(k)=k\) \(G(S;z)=\frac{z}{(1-z)^2}\)
\(S(k)=b k a^k\) \(G(S;z)=\frac{a b z}{(1-a z)^2}\)
\(S(k) = \frac{1}{k!}\) \(G(S;z)=e^z\)
\(S(k) = \left\{ \begin{array}{cc} \binom{n}{k} & 0\leq k\leq n \\ 0 & k>n \\ \end{array}\right.\) \(G(S;z)=(1+z)^n\)
\(\) \(\)
\(\) \(\)
Solve \(S(k) + 3S(k - 1) - 4S(k -2) = 0\text{,}\) \(k\geq 2\text{,}\) with \(S(0) = 3\) and \(S(1) = -2\text{.}\) The solution will be derived using the same steps that were used earlier in this section, with one variation.
  1. Translate to an equation about generating functions. First, we change the index of the recurrence relation by substituting \(n + 2\) for \(k\text{.}\) The result is \(S(n + 2) + 3S(n + 1) - 4S(n) = 0\text{,}\) \(n \geq 0\text{.}\) Now, if \(V(n) = S(n + 2) + 3 S(n + 1) - 4S(n)\text{,}\) then \(V\) is the zero sequence, which has a zero generating function. Furthermore, \(V = S\uparrow 2+3(S\uparrow )-4 S\text{.}\) Therefore,
    \begin{equation*} \begin{split} 0 &= G(V;z) \\ & = G(S\uparrow 2; z) + 3 G(S\uparrow ;z) - 4G(S;z) \\ & = \frac{G(S;z) - S(0) - S(1)z }{z^2}+4 \frac{(G(S;z) - S(0))}{z} - 4G(S;z)\\ \end{split} \end{equation*}
  2. We want to now solve the following equation for \(G(S;z)\text{:}\)
    \begin{equation*} \frac{G(S;z) - S(0) - S(1)z }{z^2}+4 \frac{(G(S;z) - S(0))}{z} - 4G(S;z) = 0 \end{equation*}
    Multiply by \(z^2\) :
    \begin{equation*} G(S;z) - 3 + 2z + 3z(G(S;z) - 3) - 4z^2 G(S;z) = 0 \end{equation*}
    Expand and collect all terms involving \(G(S;z)\) on one side of the equation:
    \begin{equation*} \begin{array}{c} G(S;z) + 3z G(S;z) - 4z^2 G(S;z) = 3 + 7z\\ \left(1 + 3z - 4z^2 \right)G(S;z)= 3 + 7z\\ \end{array} \end{equation*}
    Therefore,
    \begin{equation*} G(S;z)= \frac{3+7z}{1 + 3z - 4z^2} \end{equation*}
  3. Determine S from its generating function. \(1 + 3z - 4z^2 = (1 + 4z) (1 - z)\) thus a partial fraction decomposition of \(G(S;z)\) would be:
    \begin{equation*} \frac{A}{1+4z}+ \frac{B}{1-z}=\frac{A z-A-4 B z-B}{(z-1) (4 z+1)} =\frac{(A+B)+(4B-A)z}{(z-1) (4 z+1)} \end{equation*}
    Therefore, \(A + B = 3\) and \(4B - A = 7\text{.}\) The solution of this set of equations is \(A = 1\) and \(B = 2\text{.}\) \(G(S;z)= \frac{1}{1+4z}+ \frac{2}{1-z}\text{.}\)
    \begin{equation*} \begin{array}{c} \frac{1}{1+4z} \textrm{ is the generating function of }S_1(n)=(-4)^n\textrm{, and}\\ \frac{2}{1-z} \textrm{ is the generating function of }S_2(n) = 2(1)^n = 2\\ \end{array} \end{equation*}
    In conclusion, since \(G(S;z) = G\left(S_1;z\right) + G\left(S _2;z\right)\text{,}\) \(S(n) = 2 + (-4)^n\text{.}\)
Let \(A = \{a, b, c, d, e\}\) and let \(A^*\) be the set of all strings of length zero or more that can be made using each of the elements of \(A\) zero or more times. By the generalized rule of products, there are \(5^n\) such strings that have length \(n\text{,}\) \(n\geq 0\text{,}\) Suppose that \(X_n\) is the set of strings of length \(n\) with the property that all of the \(a\)’s and \(b\)’s precede all of the \(c\)’s, \(d\)’s, and \(e\)’s. Thus \(aaabde \in X_6\text{,}\) but \(abcabc \notin X_6\text{.}\) Let \(R(n) =\lvert X_n \rvert\text{.}\) A closed form expression for \(R\) can be obtained by recognizing \(R\) as the convolution of two sequences. To illustrate our point, we will consider the calculation of \(R(6)\text{.}\)
Note that if a string belongs to \(X_6\text{,}\) it starts with \(k\) characters from \(\{a, b\}\) and is followed by \(6 - k\) characters from \(\{c, d, e\}\text{.}\) Let \(S(k)\) be the number of strings of \(a\)’s and \(b\)’s with length \(k\) and let \(T(k)\) be the number of strings of \(c\)’s, \(d\)’s, and \(e\)’s with length \(k\text{.}\) By the generalized rule of products, \(S(k) = 2^k\) and \(T(k) = 3^k\text{.}\) Among the strings in \(X_6\) are the ones that start with two \(a\)’s and \(b\)’s and end with \(c\)’s, \(d\)’s, and \(e\)’s. There are \(S(2)T(4)\) such strings. By the law of addition,
\begin{equation*} \lvert X_6 \rvert =R(6)=S(0)T(6)+S(1)T(5)+\cdots +S(5)T(1)+S(6)T(0) \end{equation*}
Note that the sixth term of R is the sixth term of the convolution of \(S\) with \(T\text{,}\) \(S*T\text{.}\) Think about the general situation for a while and it should be clear that \(R =S*T\text{.}\) Now, our course of action will be to:
  1. Determine the generating functions of \(S\) and \(T\text{,}\)
  2. Multiply \(G(S;z)\) and \(G(T;z)\) to obtain \(G(S*T;z) = G(R;z)\text{,}\) and
  3. Determine \(R\) on the basis of \(G(R;z)\text{.}\)
  1. \(G(S;z) =\sum_{k=0}^{\infty} 2^k z^k=\frac{1}{1-2z}\) , and \(G(T;z) =\sum_{k=0}^{\infty} 3^k z^k=\frac{1}{1-3z}\)
  2. \(\displaystyle G(R;z) = G(S;z)G(T;z) = \frac{1}{(1-2z)(1-3z)}\)
  3. To recognize \(R\) from \(G(R;z)\text{,}\) we must do a partial fractions decomposition:
    \begin{equation*} \frac{1}{(1-2z)(1-3z)}=\frac{A}{1-2z}+\frac{B}{1-3z}=\frac{-3 A z+A-2 B z+B}{(2 z-1) (3 z-1)}=\frac{(A+B)+(-3 A -2 B )z}{(2 z-1) (3 z-1)} \end{equation*}
    Therefore, \(A + B = 1\) and \(-3A - 2B = 0\text{.}\) The solution of this pair of equations is \(A = - 2\) and \(B = 3\text{.}\) Since \(G(R;z) =\frac{-2}{1-2z}+\frac{3}{1-3z}\text{,}\) which is the sum of the generating functions of \(-2(2)^k\) and \(3 (3)^k\text{,}\) \(R(k) =-2(2)^k+3 (3)^k = 3^{k+1}-2^{k+1}\)
    For example, \(R(6) = 3^7 - 2^7= 2187 - 128 = 2059\text{.}\) Naturally, this equals the sum that we get from \((S*T)(6)\text{.}\) To put this number in perspective, the total number of strings of length 6 with no restrictions is \(5^6=15625\text{,}\) and \(\frac{2059}{15625}\approx 0.131776\text{.}\) Therefore approximately 13 percent of the strings of length 6 satisfy the conditions of the problem.

Subsection 8.5.6 Extra for Experts

The remainder of this section is intended for readers who have had, or who intend to take, a course in combinatorics. We do not advise that it be included in a typical course. The method that was used in the previous example is a very powerful one and can be used to solve many problems in combinatorics. We close this section with a general description of the problems that can be solved in this way, followed by some examples.
Consider the situation in which \(P_1\text{,}\) \(P_2\text{,}\) \(\ldots\text{,}\) \(P_m\) are \(m\) actions that must be taken, each of which results in a well-defined outcome. For each \(k = 1,2, . . . ,m\) define \(X_k\) to be the set of possible outcomes of \(P_k\) . We will assume that each outcome can be quantified in some way and that the quantification of the elements of \(X_k\) is defined by the function \(Q_k : X_k \to \{0, 1,2, . . .\}\text{.}\) Thus, each outcome has a non-negative integer associated with it. Finally, define a frequency function \(F_k : \{0, 1, 2, . . .\} \to \{0, 1, 2, . . .\}\) such that \(F_k(n)\) is the number of elements of \(X_k\) that have a quantification of \(n\text{.}\)
Now, based on these assumptions, we can define the problems that can be solved. If a process \(P\) is defined as a sequence of actions \(P_1,P_2,\ldots ,P_m\) as above, and if the outcome of \(P\text{,}\) which would be an element of \(X_1\times X_2\times \cdots \times X_m\text{,}\) is quantified by
\begin{equation*} Q\left(a_1,a_2, \ldots , a_m\right)= \sum_{k=1}^m Q_k\left(a_k\right) \end{equation*}
then the frequency function, \(F\text{,}\) for \(P\) is the convolution of the frequency functions for\(P_1\text{,}\) \(P_2\text{,}\) \(\ldots\text{,}\) \(P_m\text{,}\) which has a generating function equal to the product of the generating functions of the frequency functions \(F_1\text{,}\) \(F_2\text{,}\) \(\ldots\text{,}\) \(F_m\text{.}\) That is,
\begin{equation*} G(F;z) =G\left(F_1;z\right)G\left(F_2;z\right) \cdots \left(F_m;z\right) \end{equation*}
Suppose that you roll a die two times and add up the numbers on the top face for each roll. Since the faces on the die represent the integers 1 through 6, the sum must be between 2 and 12. How many ways can any one of these sums be obtained? Obviously, 2 can be obtained only one way, with two 1’s. There are two sequences that yield a sum of 3: 1-2 and 2-1. To obtain all of the frequencies with which the numbers 2 through 12 can be obtained, we set up the situation as follows. For \(j = 1, 2\text{;}\) \(P_j\) is the rolling of the die for the \(j^{\text{th}}\) time. \(X_j = \{1, 2, . . . , 6\}\) and \(Q_j : X_j \rightarrow \{0, 1, 2, 3,\ldots \}\) is defined by \(Q_j(x) = x\text{.}\) Since each number appears on a die exactly once, the frequency function is \(F_j(k)=1\) if \(1 \leq k \leq 6\text{,}\) and \(F_j(k) = 0\) otherwise. The process of rolling the die two times is quantified by adding up the \({Q_j}'s\text{;}\) that is, \(Q\left(a_1, a_2\right) =Q_{1}\left(a_1\right)+Q_2\left(a_2\right)\) . The generating function for the frequency function of rolling the die two times is then
\begin{equation*} \begin{split} G(F; z) & = G\left(F_1;z\right)G\left(F_2;z\right)\\ & = (z^6+z^5+z^4+z^3+z^2+z)^2\\ & =z^{12}+2 z^{11}+3 z^{10}+4 z^9+5 z^8+6 z^7+5 z^6+4 z^5+3 z^4+2 z^3+z^2 \end{split} \end{equation*}
Now, to get \(F(k)\text{,}\) just read the coefficient of \(z^k\text{.}\) For example, the coefficient of \(z^5\) is 4, so there are four ways to roll a total of 5.
To apply this method, the crucial step is to decompose a large process in the proper way so that it fits into the general situation that we’ve described.
Suppose that an organization is divided into three geographic sections, A, B, and C. Suppose that an executive committee of 11 members must be selected so that no more than 5 members from any one section are on the committee and that Sections A, B, and C must have minimums of 3, 2, and 2 members, respectively, on the committee. Looking only at the number of members from each section on the committee, how many ways can the committee be made up? One example of a valid committee would be 4 A’s, 4 B’s, and 3 C’s.
Let \(P_A\) be the action of deciding how many members (not who) from Section A will serve on the committee. \(X_A= \{3, 4, 5\}\) and \(Q_A(k)=k\text{.}\) The frequency function, \(F_A\) , is defined by \(F_A(k)=1\) if \(k\in X_k\) , with \(F_A(k)=0\) otherwise. \(G\left(F_A;z\right)\) is then \(z^3+ z^4+z^5\) . Similarly, \(G\left(F_B;z\right) =z^2+ z^3+ z ^4 + z^5= G\left(F_C ;z\right)\text{.}\) Since the committee must have 11 members, our answer will be the coefficient of \(z^{11}\) in \(G\left(F_A;z\right)G\left(F_B;z\right)G\left(F_C;z\right)\text{,}\) which is 10.

Exercises 8.5.7 Exercises

1.

What sequences have the following generating functions?
  1. 1
  2. \(\displaystyle \frac{10}{2-z}\)
  3. \(\displaystyle 1 + z\)
  4. \(\displaystyle \frac{3}{1+2z}+ \frac{3}{1-3z}\)
Answer.
  1. \(\displaystyle 1,0,0,0,0,\ldots\)
  2. \(\displaystyle 5(1/2)^k\)
  3. \(\displaystyle 1,1,0,0,0,\ldots\)
  4. \(\displaystyle 3(-2)^k+3\cdot 3^k\)

2.

What sequences have the following generating functions?
  1. \(\displaystyle \frac{1}{1+z}\)
  2. \(\displaystyle \frac{1}{4-3z}\)
  3. \(\displaystyle \frac{2}{1-z}+ \frac{1}{1+z}\)
  4. \(\displaystyle \frac{z+2}{z+3}\)

3.

Find closed form expressions for the generating functions of the following sequences:
  1. \(\displaystyle V(n) = 9^n\)
  2. \(P\text{,}\) where \(P(k) - 6 P(k - 1) + 5 P(k - 2) = 0\) for \(k \geq 2\text{,}\) with \(P(0) = 2\) and \(P(1) = 2\text{.}\)
  3. The Fibonacci sequence: \(F(k + 2) = F(k + 1) + F(k)\text{,}\) \(k \geq 0\text{,}\) with \(F(0) = F(1) = 1\text{.}\)
Answer.
  1. \(\displaystyle 1/(1-9z)\)
  2. \(\displaystyle (2-10z)\left/\left(1-6z+5z^2\right)\right.\)
  3. \(\displaystyle 1\left/\left(1-z-z^2\right)\right.\)

4.

Find closed form expressions for the generating functions of the following sequences:
  1. \(W(n) = \binom{5}{n} 2^n\) for \(0 \leq n \leq 5\) and \(W(n) = 0\) for \(n > 5\text{.}\)
  2. \(Q\text{,}\) where \(Q(k) + Q(k - 1) - 42Q(k - 2) = 0\) for \(k\geq 2\text{,}\) with \(Q(0) = 2\) and \(Q(1) = 2\text{.}\)
  3. \(G\text{,}\) where \(G(k + 3) = G(k + 2) + G(k + 1) + G(k)\) for \(k \geq 0\text{,}\) with \(G(0) = G(1) = G(2) = 1\text{.}\)

5.

For each of the following expressions, find the partial fraction decomposition and identify the sequence having the expression as a generating function.
  1. \(\displaystyle \frac{5+2z}{1-4z^2}\)
  2. \(\displaystyle \frac{32-22z}{2-3z+z^2}\)
  3. \(\displaystyle \frac{6-29z}{1-11z+ 30z^2}\)
Answer.
  1. \(\displaystyle 3/(1-2z)+2/(1+2z), 3\cdot 2^k+2(-2)^k\)
  2. \(\displaystyle 10/(1-z)+12/(2-z), 10+6(1/2)^k\)
  3. \(\displaystyle -1/(1-5z)+7/(1-6z), 7\cdot 6^k-5^k\)

6.

Find the partial fraction decompositions and identify the sequence having the following expressions:
  1. \(\displaystyle \frac{1}{1-9z^2}\)
  2. \(\displaystyle \frac{1+3z}{16-8z+z^2}\)
  3. \(\displaystyle \frac{2z}{1-6z-7z^2}\)

7.

Given that \(S(k) = k\) and \(T(k) = 10k\text{,}\) what is the \(k^{\text{th}}\) term of the generating function of each of the following sequences:
  1. \(\displaystyle S + T\)
  2. \(\displaystyle S\uparrow * T\)
  3. \(\displaystyle S * T\)
  4. \(\displaystyle S\uparrow *S\uparrow\)
Answer.
  1. \(\displaystyle 11k\)
  2. \(\displaystyle (5/3)k(k+1)(2k+1)+5k(k+1)\)
  3. \(\underset{j=0}{\overset{k}{\Sigma }}(j)(10(k-j))=10k\underset{j=0}{\overset{k}{\Sigma }}j-10\underset{j=0}{\overset{k}{\Sigma }}j^2\) \(=5k^2(k+1)-(5k(k+1)(2k+1)/6) =(5/3)k(k+1)(2k+1)\)
  4. \(\displaystyle k(k+1)(2k+7)/12\)

8.

Given that \(P(k) = \binom{10}{k}\) and \(Q(k) = k!\text{,}\) what is the \(k^{\text{th}}\) term of the generating function of each of the following sequences:
  1. \(\displaystyle P * P\)
  2. \(\displaystyle P + P\uparrow\)
  3. \(\displaystyle P * Q\)
  4. \(\displaystyle Q * Q\)

9.

A game is played by rolling a die five times. For the \(k^{\text{th}}\) roll, one point is added to your score if you roll a number higher than \(k\text{.}\) Otherwise, your score is zero for that roll. For example, the sequence of rolls \(2,3,4,1,2\) gives you a total score of three; while a sequence of 1,2,3,4,5 gives you a score of zero. Of the \(6^5 = 7776\) possible sequences of rolls, how many give you a score of zero?, of one? \(\ldots \) of five?
Answer.
Coefficients of \(z^0\) through \(z^5\) in \((1+5z)(2+4z)(3+3z)(4+2z)(5+z)\)
\(\begin{array}{cc} k & \textrm{ Number of ways of getting a score of } k \\ 0 & 120 \\ 1 & 1044 \\ 2 & 2724 \\ 3 & 2724 \\ 4 & 1044 \\ 5 & 120 \\ \end{array}\)

10.

Suppose that you roll a die ten times in a row and record the square of each number that you roll. How many ways could the sum of the squares of your rolls equal 40? What is the most common outcome?
<Prev^TopNext>