The topic of spanning trees is motivated by a graph-optimization problem.
A graph of Atlantis University (Figure 10.2.1) shows that there are four campuses in the system. A new secure communications system is being installed and the objective is to allow for communication between any two campuses; to achieve this objective, the university must buy direct lines between certain pairs of campuses. Let \(G\) be the graph with a vertex for each campus and an edge for each direct line. Total communication is equivalent to \(G\) being a connected graph. This is due to the fact that two campuses can communicate over any number of lines. To minimize costs, the university wants to buy a minimum number of lines.
Figure10.2.1.Atlantis University Graph
The solutions to this problem are all trees. Any graph that satisfies the requirements of the university must be connected, and if a cycle does exist, any line in the cycle can be deleted, reducing the cost. Each of the sixteen trees that can be drawn to connect the vertices North, South, East, and West (see Exercise 10.1.3.1) solves the problem as it is stated. Note that in each case, three direct lines must be purchased. There are two considerations that can help reduce the number of solutions that would be considered.
Objective 1: Given that the cost of each line depends on certain factors, such as the distance between the campuses, select a tree whose cost is as low as possible.
Objective 2: Suppose that communication over multiple lines is noisier as the number of lines increases. Select a tree with the property that the maximum number of lines that any pair of campuses must use to communicate with is as small as possible.
Typically, these objectives are not compatible; that is, you cannot always simultaneously achieve these objectives. In the case of the Atlantis university system, the solution with respect to Objective 1 is indicated with solid lines in Figure 10.2.1. There are four solutions to the problem with respect to Objective 2: any tree in which one campus is directly connected to the other three. One solution with respect to Objective 2 is indicated with dotted lines in Figure 10.2.1. After satisfying the conditions of Objective 2, it would seem reasonable to select the cheapest of the four trees.
Subsection10.2.2Definition
Definition10.2.2.Spanning Tree.
Let \(G = (V, E)\) be a connected undirected graph. A spanning tree for \(G\) is a spanning subgraph 9.1.17 of \(G\) that is a tree.
Note10.2.3.
If \((V, E')\) is a spanning tree, \(\lvert E' \rvert =\lvert V \rvert - 1\text{.}\)
The significance of a spanning tree is that it is a minimal spanning set. A smaller set would not span the graph, while a larger set would have a cycle, which has an edge that is superfluous.
For the remainder of this section, we will discuss two of the many topics that relate to spanning trees. The first is the problem of finding Minimal Spanning Trees, which addresses Objective 1 above. The second is the problem of finding Minimum Diameter Spanning Trees, which addresses Objective 2.
Definition10.2.4.Minimal Spanning Tree.
Given a weighted connected undirected graph \(G = (V, E, w)\text{,}\) a minimal spanning tree is a spanning tree \((V, E')\) for which \(\sum_{e\in E'} w(e)\) is as small as possible.
Subsection10.2.3Prim’s Algorithm
Unlike many of the graph-optimization problems that we’ve examined, a solution to this problem can be obtained efficiently. It is a situation in which a greedy algorithm works.
Definition10.2.5.Bridge.
Let \(G = (V, E)\) be an undirected graph and let \(\{L, R\}\) be a partition of \(V\text{.}\) A bridge between \(L\) and \(R\) is an edge in \(E\) that connects a vertex in \(L\) to a vertex in \(R\text{.}\)
Theorem10.2.6.
Let \(G = (V, E, w)\) be a weighted connected undirected graph. Let \(V\) be partitioned into two sets \(L\) and \(R\text{.}\) If \(e^*\) is a bridge of least weight between \(L\) and \(R\text{,}\) then there exists a minimal spanning tree for \(G\) that includes \(e^*\text{.}\)
Suppose that no minimal spanning tree including \(e^*\) exists. Let \(T = (V, E')\) be a minimal spanning tree. If we add \(e^*\) to \(T\text{,}\) a cycle is created, and this cycle must contain another bridge, \(e\text{,}\) between \(L\) and \(R\text{.}\) Since \(w\left(e^*\right) \leq w(e)\text{,}\) we can delete \(e\) and the new tree, which includes \(e^*\) must also be a minimal spanning tree.
The bridges between the vertex sets \(\{a, b, c\}\) and \(\{d, e\}\) in Figure 10.2.8 are the edges \(\{b, d\}\) and \(\{c, e\}\text{.}\) According to the theorem above, a minimal spanning tree that includes \(\{b, d\}\) exists. By examination, you should be able to see that this is true. Is it true that only the bridges of minimal weight can be part of a minimal spanning tree?
Figure10.2.8.Bridges between two sets
Theorem 10.2.6 essentially tells us that a minimal spanning tree can be constructed recursively by continually adding minimally weighted bridges to a set of edges.
Algorithm10.2.9.Prim’s Algorithm.
Let \(G = (V, E, w)\) be a connected, weighted, undirected graph, and let \(v_0\) be an arbitrary vertex in \(V\text{.}\) The following steps lead to a minimal spanning tree for \(G\text{.}\)\(L\) and \(R\) will be sets of vertices and \(E'\) is a set of edges.
(Initialize) \(L = V - \left\{v_0\right\}\text{;}\)\(R = \left\{v_0\right\}\text{;}\)\(E' = \emptyset\text{.}\)
(Build the tree) While \(L\neq \emptyset\text{:}\)
Find \(e^* = \left\{v_L,v_R\right\}\text{,}\) a bridge of minimum weight between \(L\) and \(R\text{.}\)
\(R = R \cup \left\{v_L \right\}\text{;}\)\(L = L - \left\{v_L\right\}\) ; \(E' =E'\cup \left\{e^*\right\}\)
Terminate with a minimal spanning tree \((V, E')\text{.}\)
Note10.2.10.
If more than one minimal spanning tree exists, then the one that is obtained depends on \(v_0\) and the means by which \(e^*\) is selected in Step 2.
Warning: If two minimally weighted bridges exist between \(L\) and \(R\text{,}\) do not try to speed up the algorithm by adding both of them to \(E\)’.
If it is not known whether \(G\) is connected, Algorithm 10.2.9 can be revised to handle this possibility. The key change (in Step 2.1) would be to determine whether any bridge at all exists between \(L\) and \(R\text{.}\) The condition of the while loop in Step 2 must also be changed somewhat.
Consider the graph in Figure 10.2.12. If we apply Prim’s Algorithm starting at \(a\text{,}\) we obtain the following edge list in the order given: \(\{a, f\}, \{f, e\}, \{e, c\}, \{c, d\}, \{f, b\}, \{b, g\}\text{.}\) The total of the weights of these edges is 20. The method that we have used (in Step 2.1) to select a bridge when more than one minimally weighted bridge exists is to order all bridges alphabetically by the vertex in \(L\) and then, if further ties exist, by the vertex in \(R\text{.}\) The first vertex in that order is selected in Step 2.1 of the algorithm.
Figure10.2.12.A small weighted graph
Definition10.2.13.Minimum Diameter Spanning Tree.
Given a connected undirected graph \(G = (V, E)\text{,}\) find a spanning tree \(T = (V, E')\) of \(G\) such that the longest path in \(T\) is as short as possible.
The Minimum Diameter Spanning Tree Problem is trivial to solve in a \(K_n\text{.}\) Select any vertex \(v_0\) and construct the spanning tree whose edge set is the set of edges that connect \(v_0\) to the other vertices in the \(K_n\) . Figure 10.2.15 illustrates a solution for \(n=5\text{.}\)
Figure10.2.15.Minimum diameter spanning tree for \(K_5\)
For incomplete graphs, a two-stage algorithm is needed. In short, the first step is to locate a “center” of the graph. The maximum distance from a center to any other vertex is as small as possible. Once a center is located, a breadth-first search of the graph is used to construct the spanning tree.
Exercises10.2.4Exercises
1.
Suppose that after Atlantis University’s phone system is in place, a fifth campus is established and that a transmission line can be bought to connect the new campus to any old campus. Is this larger system the most economical one possible with respect to Objective 1? Can you always satisfy Objective 2?
It might not be most economical with respect to Objective 1. You should be able to find an example to illustrate this claim. The new system can always be made most economical with respect to Objective 2 if the old system were designed with that objective in mind.
2.
Construct a minimal spanning tree for the capital cities in New England (see Table 9.5.3).
3.
Show that the answer to the question posed in Example 10.2.7 is “no.”
In the figure below, \(\{1,2\}\) is not a minimal bridge between \(L=\{1,4\} \textrm{ and } R=\{2,3\}\text{,}\) but it is part of the minimal spanning tree for this graph.
Figure10.2.16.
4.
Find a minimal spanning tree for the following graphs.
Figure10.2.17.
Figure10.2.18.
Figure10.2.19.
5.
Find a minimum diameter spanning tree for the following graphs.
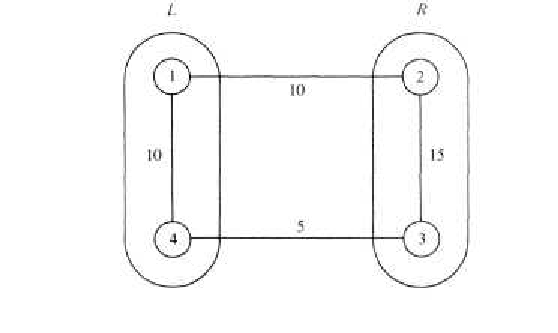
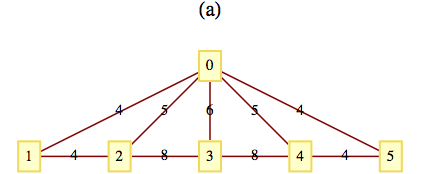
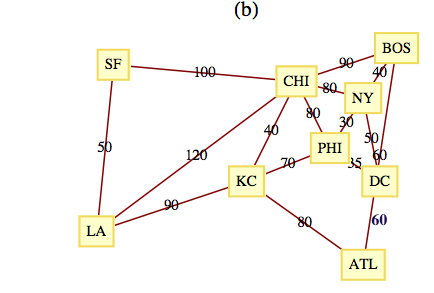
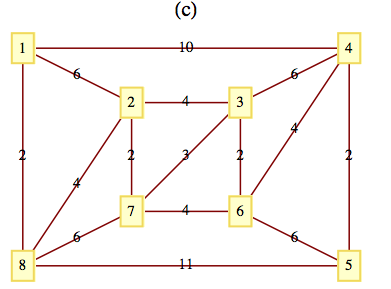
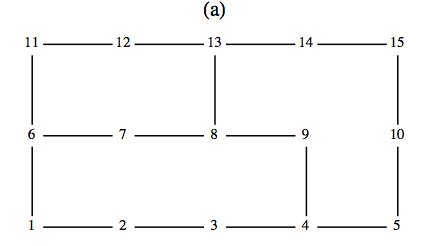
Edges in one solution are: \(\{8,7\},\{8,9\},\{8,13\},\{7,6\},\{9,4\},\{13,12\},\{13,14\},\{6,11\},\{6,1\},\{1,2\},\{4,3\},\{4,5\},\{14,15\},
\textrm{ and } \{5,10\}\)
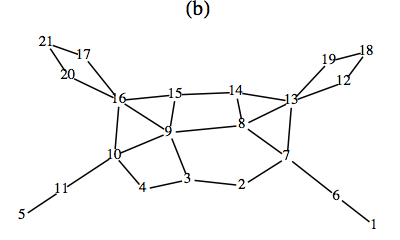
Vertices 8 and 9 are centers of the graph. Starting from vertex 8, a minimum diameter spanning tree is \(\{\{8, 3\}, \{8, 7\}, \{8, 13\},
\{8, 14\}, \{8, 9\}, \{3, 2\}, \{3, 4\}, \{7, 6\}, \{13, 12\}, \{13, 19\}, \{14, 15\}, \{9, 16\}, \{9, 10\}, \{6, 1\}, \{12, 18\}, \{16, 20\}, \{16,
17\}, \{10, 11\}, \{20, 21\}, \{11, 5\}\}.\) The diameter of the tree is 7.
6.
In each of the following parts justify your answer with either a proof or a counterexample.
Suppose a weighted undirected graph had distinct edge weights. Is it possible that no minimal spanning tree includes the edge of minimal weight?
Suppose a weighted undirected graph had distinct edge weights. Is it possible that every minimal spanning tree includes the edge of maximal weight? If true, under what conditions would it happen?
