Composite Quadratic Lyapunov Functions

Lyapunov functions are not only essential to stability analysis, but are also powerful tools for assessment of
various performances, such as robustness, disturbance rejection and forced oscillations.  Quadratic Lyapunov functions have been extensively exploited since they are simple and usually lead to Linear Matrix Inequality
(LMI) conditions, which are numerically tractable.  Since it is well recognized that quadratic functions can be
very conservative, better evaluation of system performances and further improvement of system design rely on
the development of non-quadratic Lyapunov functions which are theoretically effective and numerically tractable.  

A composite quadratic function is constructed from a family of quadratic functions via a certain operation
between these quadratic functions. We consider three types of operations: taking the maximum, the minimum
or the convex hull of the quadratic functions. The three resulting functions are called the max function,
the min function and the convex hull functions, respectively.

Given positive definite matrices, P₁, P₂, ..., P_J. The  min function is defined as,
                                  V_min(x):= ½ min {x'P_j x: j=1,2,...,J};
The max function is, 
                                  V_max(x):= ½ max {x'P_j x: j=1,2,...,J};
The convex hull function is,
                             V_c(x) = ½ min {x'(g₁P₁+g₂P₂+...+g_JP_J)^-1x:  g₁+g₂+...+g_J=1, g_j≥0}.
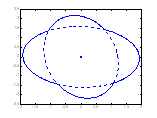
For a positive definite function V(x), its 1-level set is defined as L_V={x: V(x)≤1}. The level set of a quadratic
function is an ellipsoid; the level set of the min function is the union of ellipsoids; the level set of the max
function is the intersection of ellipsoids; the level set of the convex  hull function is the convex hull of ellipsoids.
See below:

 

 
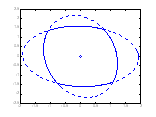
      L_Vmin= {x: V_min(x)≤1}                     L_Vmax= {x: V_max(x)≤1}                     L_Vc= {x: V_c(x)≤1}

The max function and the convex hull function are conjugate types. They have been applied to stability and
performance analysis/design of saturated systems and  linear differential inclusions (LDIs, usually used for
description of time varying uncertain systems). All of the three functions have been used for designing switching
laws for switched systems. The following is a list of recent works on the development and application of
these composite quadratic functions.

1. T. Hu, L. Ma and Z. Lin, ``On several composite quadratic Lyapunov

   functions for switched systems," IEEE Conference on Decision and Control, 2006. 

2. T. Hu, ``Nonlinear control design for linear differential inclusions via
   convex hull of quadratics," Automatica, to appear. 

3. T. Hu, A. R. Teel and L. Zaccarian, ``Stability and performance for saturated systems 
   via quadratic and non-quadratic Lyapunov functions," IEEE Transactions on Automatic Control, 
   51(11), pp.~1770-1786, 2006.

4. R. Goebel, A.R. Teel, T. Hu and Z. Lin, ``Conjugate convex Lyapunov functions for dual linear 

   differential equations," IEEE Transactions on Automatic Control, 51(4), pp.661-666, 2006.

5. T. Hu, R. Goebel, A. R. Teel and Z. Lin, ``Conjugate Lyapunov functions for saturated linear systems," 

   Automatica, 41(11), pp.1949-1956, 2005.

6. T. Hu and Z. Lin, ``Absolute stability analysis of discrete-time systems with

   composite quadratic Lyapunov functions," IEEE Transactions on Automatic Control, Vol.50, 
   pp.781-797, 2005.

7. T. Hu and Z. Lin, ``Properties of the composite quadratic Lyapunov functions," 
   IEEE Transactions on Automatic Control, Vol.49, No.7, pp.1162-1167, 2004. 
   pp.1249-1253, 2003. 

8. T. Hu and Z. Lin, ``Composite quadratic Lyapunov functions for constrained control systems," 
   IEEE Transactions on Automatic Control, Vol.48, No.3, pp.440-450, March 2003.